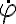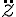Duda sobre "ecuaciones del movimiento" y derivar "L"

Duda sobre "ecuaciones del movimiento" y derivar "L"

de Ivan Pablo Martinez Gamba -
Número de respuestas: 2

Buenas, tengo un par de dudas.

La primera es, cómo interpretar la pregunta "Hallar las ecuaciones de movimiento", por ejemplo en el ejercicio 7, no comprendo si tengo que hallar las ecuaciones de movimiento de P, de Q, o de todo el sistema. Además me gustaría saber en que puedo dejar expresada las ecuaciones de movimiento.

La segunda duda es, a la hora de hallar las ecuaciones de movimiento puedo optar por usar el momento angular (usando que se conserva), puedo llegar a mr^2.dphi/dt=l, l constante, obteniendo así, una ecuación de movimiento. Si derivo eso, obtengo otra expresión, pero no sé si puedo considerar esta derivada como una ecuación de movimiento o si ya se ve incluida en la primer expresión que mencioné.

Gracias, saludos!

En respuesta a Ivan Pablo Martinez Gamba

Re: Duda sobre "ecuaciones del movimiento" y derivar "L"

de Ricardo Marotti -

Estimado:

En la parte a del Ejercicio 7, estrictamente pediría hallar las ecuaciones de movimiento de P y de Q por separado. Pero como el hilo es inextensible la altura de Q, z, y la coordenada radial de P, ρ, son iguales a menos de una constante. Eligiendo bien el nivel de referencia de la altura de Q se puede hacer la constante nula. Por lo tanto las coordenadas son iguales y verificarán la misma ecuación de movimiento. En este mismo ejercicio esa ecuación de movimiento queda expresada en función de ρ,  \ddot{ \rho } ,  \dot{ \varphi } y  \ddot{z} . Se halla de aplicar la segunda ley de Newton a P, a Q por separado; y proyectar la primera según la dirección radial y la segunda según la dirección vertical (siendo la tensión del hilo la misma). Utilizando el vínculo anterior z = ρ y la conservación del momento angular, se puede escribir una ecuación de movimiento solo en ρ y su derivada segunda, que es lo que se precisa para hacer la parte siguiente. 

Cuando se pide una ecuación de movimiento, lo que se pide es una ecuación que implica derivadas segundas en el tiempo. Esto es porque se obtiene de proyectar la segunda ley de Newton según alguna o algunas direcciones convenientemente elegidas. Cuando tenemos ecuaciones diferenciales que no involucran derivadas segundas en el tiempo, sino solo derivadas primeras en el tiempo (como la conservación del momento angular o el teorema de la energía) decimos que tenemos preintegrales de movimiento o leyes de conservación. No serían exactamente ecuaciones de movimiento. Estrictamente para hallar las ecuaciones de movimiento deberíamos derivar respecto al tiempo esas preintegrales. Pero usualmente las preintegrales tienen más información que las ecuaciones de movimiento, porque incluyen constantes que dependen de las condiciones iniciales. Y derivar es una operación más fácil que preintegrar. Por lo que dar las preintegrales es un paso más adelante que dar las ecuaciones de movimiento. Y muchas veces si se piden ecuaciones de movimiento, alcanza con dar las preintegrales de movimiento como respuesta. O sea, la respuesta a esa pregunta sería correcta. A menos que, como en la parte b del EJercicio que mencionabas, se precise realmente la ecuación de movimiento para hacerlo. Si no hiciste la derivación en la parte a, tendrás que hacerla en la parte b. 

Saludos: 

Ricardo.