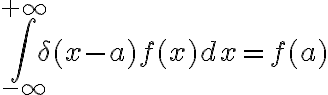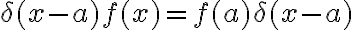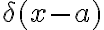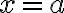Práctico 5 - Ejercicio 3

Práctico 5 - Ejercicio 3

de Nicolas Aguilera Leal -
Número de respuestas: 2

Buenas,

Estaba viendo la solución de la parte a) del ejercicio, y no me queda claro qué propiedad usaron para calcular (por ejemplo) la integral 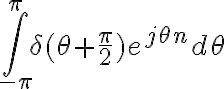\int_{-\pi}^{\pi}\delta(\theta+\frac{\pi}{2})e^{j\theta n}d\theta

Lo que intenté hacer yo cuando llegué a ese punto en el ejercicio fue usar la siguiente propiedad de la delta 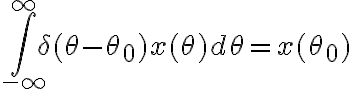\int_{-\infty}^{\infty}\delta(\theta-\theta_0)x(\theta)d\theta = x(\theta_0) . Sin embargo no podría porque el intervalo de integración de mi integral es finito.

Se cumple en este caso que 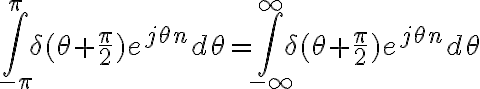\int_{-\pi}^{\pi}\delta(\theta+\frac{\pi}{2})e^{j\theta n}d\theta = \int_{-\infty}^{\infty}\delta(\theta+\frac{\pi}{2})e^{j\theta n}d\theta ? La solución me da a entender que sí. Si es así, por qué? Hay algo que no estoy viendo?

Saludos!
En respuesta a Nicolas Aguilera Leal

Re: Práctico 5 - Ejercicio 3

de Santiago Martinez -
Hola Nicolás,
creo que la respuesta se puede dividir en dos partes independientes.

Como ya sabes, las deltas de tiempo contínuo son objetos matemáticos bastante especiales y entrar en sus detalles más profundos requeriría un análisis mucho más amplio del que quisiéramos darle aquí. El resultado que tu planteas (\int_{-\infty }^{+\infty}\delta(x-a)f(x)dx = f(a) ) es correcto y es equivalente a decir que \delta(x-a)f(x)= f(a)\delta(x-a). Por otro lado, la integral de \delta(x-a) es 1 si el intervalo de integración contiene al asiento de la delta (en este caso x=a), por lo que la propiedad se seguirá cumpliendo si el intervalo de integración "contiene al asiento de \delta".

Por otro lado, recordá que las transformadas obtenidas mediante la DTFT son periódicas de período 2\pi, por lo que la última igualdad que planteas no se puede cumplir (\delta(\theta + \pi/2) es un tren de deltas con distancia 2\pi entre ellas).

Saludos y si algo no quedó claro la seguimos por acá