Buenas, en este ejercicio en la solución no me queda claro por qué al ver la salida total de la entrada trasladada el primer (-1)^k no me queda elevado a la k-N0
Hola:
El caso que se analiza allí es cuando se retarda la entrada, sería x[n-N_0]. La razón por la que no se retarda el -1^n es que eso no es la entrada, es algo que depende de n pero que es parte de nuestro sistema.
Dicho de otra forma, por más que se retarde la entrada los valores por los que se va a multiplicar la entrada retardada en ese primer paso del sistema completo, no dependen del retardo de la entrada sino solo del instante n (o k que es la variable temporal que se usó en la ecuación de abajo.)
Si no queda claro decinos y vemos de verlo con un ejemplo particular.
Saludos,
Pablo
en este contexto de tiempo discreto, "n" es la variable "temporal", así que con ella describimos la evolución de las señales "a lo largo del tiempo". Como ejemplo
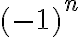 es una señal de tiempo discreto que cada valor es 1 ó -1 en forma alternada.
es una señal de tiempo discreto que cada valor es 1 ó -1 en forma alternada. ![x[n] x[n]](https://eva.fing.edu.uy/filter/tex/pix.php/d3baaa3204e2a03ef9528a7d631a4806.gif) es una señal genérica de tiempo discreto y la señal
es una señal genérica de tiempo discreto y la señal ![z[n] = x[n-N] z[n] = x[n-N]](https://eva.fing.edu.uy/filter/tex/pix.php/048309ed8771472d390a0445f3f7201d.gif) sería otra señal de tiempo discreto que se relaciona con
sería otra señal de tiempo discreto que se relaciona con ![x[n] x[n]](https://eva.fing.edu.uy/filter/tex/pix.php/d3baaa3204e2a03ef9528a7d631a4806.gif) (
( es la señal
es la señal  retrasada
retrasada 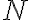 unidades de tiempo).
unidades de tiempo).Dirigiéndonos al problema en cuestión, la señal de entrada
![x[n] x[n]](https://eva.fing.edu.uy/filter/tex/pix.php/d3baaa3204e2a03ef9528a7d631a4806.gif) es multiplicada por una señal de la forma
es multiplicada por una señal de la forma 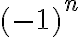 , haciendo que la entrada del sistema
, haciendo que la entrada del sistema  sea
sea ^n x[n](-1)^n](https://eva.fing.edu.uy/filter/tex/pix.php/49aaeda8311b4902c986a1709f49e695.gif) .
.Si eligiéramos otra señal de entrada,
 por ejemplo, la entrada del sistema
por ejemplo, la entrada del sistema  sería entonces
sería entonces ^n z[n](-1)^n](https://eva.fing.edu.uy/filter/tex/pix.php/0c479fc5c6211357cc0145ca5d064772.gif) .
. Si pensaramos en que queremos verificar la invarianza temporal del sistema, parte de nuestro análisis implica aplicarle al sistema completo una entrada y ella misma retrasada una cantidad $N$ genérica.
En el primer caso, la entrada el sistema
 es, naturalmente,
es, naturalmente, ^n x[n](-1)^n](https://eva.fing.edu.uy/filter/tex/pix.php/49aaeda8311b4902c986a1709f49e695.gif) .
.En el caso de la entrada retrasada, si definimos
![z[n] = x[n-N] z[n] = x[n-N]](https://eva.fing.edu.uy/filter/tex/pix.php/048309ed8771472d390a0445f3f7201d.gif) , la entrada al sistema sería
, la entrada al sistema sería ^n = x[n-N](-1)^n z[n](-1)^n = x[n-N](-1)^n](https://eva.fing.edu.uy/filter/tex/pix.php/33ee9bd855693456c851cad4b7039c35.gif) .
.Este análisis te ha podido aclarar algo?
saludos
Creo que ahí lo entendí mejor, por ejemplo si mi entrada es cos[n] cuando lo paso por la primer parte del sistema me queda cos[n].(-1)^n, si luego yo tengo una entrada z[n]=x[n-N] que queda cos[n-N] y por el razonamiento del final de la respuesta quedaría cos[n-N].(-1)^n al pasar por la primer parte del sistema. Pero entonces cos[2] como entrada sola tiene dos posibles salidas, porque en el primer caso voy a hacer cos[2].(-1)^n y eso lo meto al sistema S. Luego si N es 2 por ejemplo z[4]=x[4-2]=cos[2] pero cuando lo paso por el multiplicador me queda cos[2].(-1)^4. Eso me genera un poco de conflicto digamos, que para la misma entrada puedas tener distintas salidas.
A su vez, como duda más general capaz si tomo algo más raro tipo z[n]=x[n^2] ponele, me pasa lo mismo que al pasarlo por el (-1)^n me queda x[n^2].(-1)^n?
Graciass
Hola. Ese razonamiento falla porque ![cos[2] cos[2]](https://eva.fing.edu.uy/filter/tex/pix.php/03ba969f8d8c9547e58a53cacf86e6da.gif) no es una señal, es un número.
no es una señal, es un número.
Un sistema tiene siempre como entrada una señal (una función de variable  para el caso de tiempo discreto).
para el caso de tiempo discreto).
Además nosotros siempre trabajaremos con sistemas deterministicos, lo que significa que para una señal de entrada existe una única señal de salida (el sistema hará corresponder una entrada con una salida, pero ese mapeo es señal a señal).
Respecto a la pregunta del final: si, la entrada del sistema  será la entrada del sistema multiplicada por la función
será la entrada del sistema multiplicada por la función 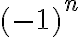 .
.
Saludos,
--Federico Lecumberry
