buenas, no logro comprender en este caso cuando tengo multiplicidad algebraica 3 y geométrica 1 como calcular la matriz cambio de base de jordan.
saludos,
Sofía
buenas, no logro comprender en este caso cuando tengo multiplicidad algebraica 3 y geométrica 1 como calcular la matriz cambio de base de jordan.
saludos,
Sofía
 lineal es
lineal es 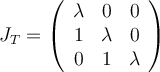
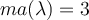 y
y 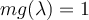 . La pregunta es como hallar una base
. La pregunta es como hallar una base 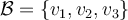 de
de  tal que
tal que 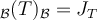 .
. y una base de Jordan. Es decir, calcular la matriz asociada a
y una base de Jordan. Es decir, calcular la matriz asociada a  y determinar su forma de Jordan. Esto lo haces primero calculando los valores propios y después los subespacios propios asociados. Cada valor propio determina un bloque de Jordan en la forma de Jordan. La multiplicidad algebraica del valor propio determina el tamaño de dicho bloque de Jordan, y su multiplicidad algebraica el número de sub-bloques de Jordan dentro del bloque de Jordan. Juntando los bloques de Jordan dentro de una matriz te queda la forma de Jordan. La base la calculas teniendo en cuenta que la columna i-ésima son las coordenadas de
y determinar su forma de Jordan. Esto lo haces primero calculando los valores propios y después los subespacios propios asociados. Cada valor propio determina un bloque de Jordan en la forma de Jordan. La multiplicidad algebraica del valor propio determina el tamaño de dicho bloque de Jordan, y su multiplicidad algebraica el número de sub-bloques de Jordan dentro del bloque de Jordan. Juntando los bloques de Jordan dentro de una matriz te queda la forma de Jordan. La base la calculas teniendo en cuenta que la columna i-ésima son las coordenadas de  en la base de Jordan, donde
en la base de Jordan, donde 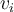 es el i-ésimo vector en dicha base.
es el i-ésimo vector en dicha base.