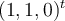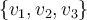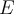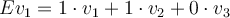Ejercicio 4) Parte E)

Ejercicio 4) Parte E)

de Bruno Tadeo Cardozo Pintos -
Número de respuestas: 3

Buenas noches, me encontraba mirando la solucion posteada a este ejercicio, y en una parte del video, para ser más preciso en el minuto 14:10, se escribe el vector faltante de la base como: 

Ev1 = v1 + v2

No me queda claro cómo llegar a esta conclusión, ando medio atrasado con el práctico y no he podido asistir a las clases esta semana, agradezco si me pueden dar una mano.
Saludos.

En respuesta a Bruno Tadeo Cardozo Pintos

Re: Ejercicio 4) Parte E)

de Jose Vivero -
Hola Bruno,

Fíjate que la primer columna de la forma de Jordan es  (1,1,0)^t y eso significa, por definición de matriz asociada, que el transformado del primer vector de la base de Jordan tiene como vector de coordenadas en esa base a (1,1,0)^t . O sea, si denotamos la base de Jordan por  \{v_1,v_2,v_3\} y la transformación por E , tendremos justamente que  Ev_1=1\cdot v_1 + 1\cdot v_2 + 0\cdot v_3 .

Espero esto te despeje la duda. Saludos
En respuesta a Bruno Tadeo Cardozo Pintos

Re: Ejercicio 4) Parte E)

de Daniel Edgardo Pellejero Morales -
Hola ¿Donde se puede ver el video? Yo no se como se haya la base de Jordan y capaz que ahí dice
En respuesta a Daniel Edgardo Pellejero Morales

Re: Ejercicio 4) Parte E)

de Marco Antonio Perez -
Daniel,

Los primeros comentarios son de 2021. Seguramente se refieren a un vídeo subido a YouTube hace un año. Desconozco el enlace. Igual te cuento que la solución a ese ejercicio la subí escrita en mis apuntes de práctico del 1 de abril. Esa clase de práctico también la grabé y subí. Puedes encontrar el enlace a la grabación en la sección de formas de Jordan (práctico de recuperación).

Saludos,
Marco