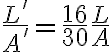ejercicio 2

ejercicio 2

de Joaquin Costa Salles -
Número de respuestas: 7

Buenas, 

Hice el ejercicio y me quedó la solución igual pero un 2 en vez del 4 que aparece en la solución. Es decir, me queda:

A' = raíz(4/30) * A     y       L' = raíz(30/4) * L

Qué puedo tener mal? Yo supuse que i'=4i y que v'=30v ,está bien eso? 

(Cuando pongo ' me refiero a final)

Gracias.

En respuesta a Joaquin Costa Salles

Re: ejercicio 2

de Juan Arrospide Orsi -
Hola, yo también estoy teniendo dificultades con este ejercicio, y cuando leí la pregunta de Joaquín me surgió una duda:
Está bien que hayas puesto v'=30v ? yo lo que entendí de la letra es que lo que se multiplica por 30 es R, de la ecuación DeltaV = R . i
Claramente me estoy equivocando yo porque no me queda igual que la respuesta correcta, pero me gustaría saber por qué está mal lo que pensé; y cual es la forma correcta de hacerlo.

Muchas gracias,

Juan.
En respuesta a Juan Arrospide Orsi

Re: ejercicio 2

de Joaquin Costa Salles -
Lo que dice la letra es: "la potencia disipada aumente en un factor de 30". La potencia es igual al voltaje por la intensidad. P=V*i. entonces yo estuve mal en hacer V'=30V.
Lo que debería haber hecho es P'=30P, que es igual a que V'*i' = 30V*i.
Como i'=4i si suplanto ahí tendría que quedar.
En respuesta a Joaquin Costa Salles

Re: ejercicio 2

de Matias Fernandez -
Gurises, les quedó al final?
En respuesta a Matias Fernandez

Re: ejercicio 2

de Agustín Arístides Almeida Ahlers -
Buenas tardes, llegué a la relacion V´=30/4V, pero no se cómo continuar de ahí, solo se que L´.a´=L.a pero no se como relacionar los parámetros que quiero hallar con esa relación, cómo podría seguir? Gracias.
En respuesta a Agustín Arístides Almeida Ahlers

Re: ejercicio 2

de Nicolás Noya -
Hola Agustín,
Para resolver este problema tenés que usar la formula que relaciona la resistencia con la conductividad, te hablo de:
R=L/(sigma*A)
Luego suplantás esta relación en la ecuación que relaciona las potencias inicial y final hasta que se obtiene una ecuación que te relaciona el largo y el área iniciales con el largo y el área finales (distinta a la que mencionaste) y con la que mencionaste arriba despejas.
Saludos, Nicolás