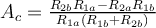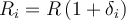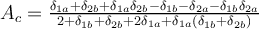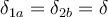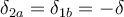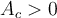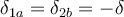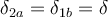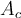Foro del curso

Hola, Mauricio,

Como bien mostras en la imagen la ganancia en modo común es:

$A_c=\frac{R_{2b}R_{1a}-R_{2a}R_{1b}}{R_{1a}\left(R_{1b}+R_{2b}\right)}$

Si reemplazas $R_{i}=R\left(1+\delta_{i}\right)$, entonces

$A_c=\frac{\delta_{1a}+\delta_{2b}+\delta_{1a}\delta_{2b}-\delta_{1b}-\delta_{2a}-\delta_{1b}\delta_{2a}}{2+\delta_{1b}+\delta_{2b}+2\delta_{1a}+\delta_{1a}\left(\delta_{1b}+\delta_{2b}\right)}$

Teniendo en cuenta que 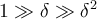$1\gg\delta\gg\delta^{2}$, en este caso vemos que el numerador no tiene término constante mientras que el denominador sí (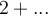$2+...$). Entonces lo más razonable es maximizar la amplitud del numerador, porque el denominador afecta menos ya que es de la forma $2+A\delta+B\delta^{2}\approx2$.

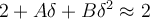Dicho esto, las 2 posibilidades son:

1. $\delta_{1a}=\delta_{2b}=\delta$
   $\delta_{2a}=\delta_{1b}=-\delta$.
   En este caso $A_c>0$.
2. $\delta_{1a}=\delta_{2b}=-\delta$
   $\delta_{2a}=\delta_{1b}=\delta$.
   En este caso $A_c$.

Probando te das cuenta de que hay uno de los 2 casos anteriores que maximiza 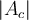$\left|A_c\right|$ porque el denominador da algo (un poco) más chico que en el otro.

Saludos