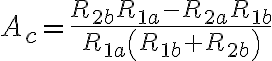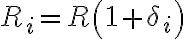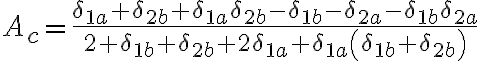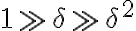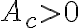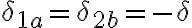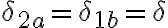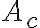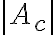Buenas,
En la parte b de este ejercicio se pide hallar la expresión para el peor caso de la ganancia en modo común. En la imagen esta el resultado de cuanto da la ganancia común y las resistencias todas toman valor R(1+-delta). Como el peor caso corresponde a un Ac alto, tengo que maximizar la expresión de Ac obtenida.
Lo que no entiendo es como hacerlo, al principio había intentado con hacer el denominador lo mas chico posible pero me quedaron resistencias que no me quedaba claro que valor debían tomar (si con el + o el -). Por otro lado, además de minimizar el denominador también existe la opción de hacer que el numerador sea lo más grande posible y entré a confundirme porque no sabía que camino tomar. Quisiera saber si lo estoy pensando bien, cuál opción sería correcta y por qué se debe hacer de esa manera.
Gracias!