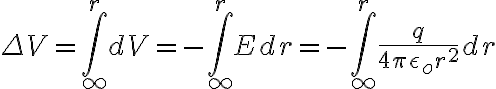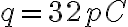Hola, para este ejercicio lo que hice fue plantear lo siguiente: dq=ρ4πr²dr
V(R)=1/4πe0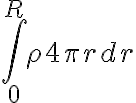
luego V(R)=ρR²/2e0.
Como ρ=q/V=3q/4πR³ entoces V(R)=3q/8πe0R de donde se despeja R=3q/8πe0V.
Supongo que algo en mi procedimiento es incorrecto porque el resultado es distinto al de las soluciones, saludos.
Pensalo nuevamente tomando en cuenta esta serie de pasos. Tené en cuenta que por fuera de la esfera uno puede verlo como si fuera una carga puntual con 
.
Si no te sale avisá.
Saludos!
Esta bien que te quede eso.
Está puesto desde dónde hasta dónde, es desde el infinito (nuestro punto de referencia en el que tomamos como que ahí el potencial es cero, lo fijamos) hasta el punto en cuestión que es r, el radio de la esfera. Es decir que vas desde el infinito hasta la cáscara de la esfera.
Se entendió?
Saludos
Se entendió, gracias. No me daba cuenta de que cuando lo evalúo en el infinito ese termino tiende a cero.
Para definir el potencial se toma como que en el infinito vale 0. Es como cuando en física 1 tomabas una altura para definir que a esa altura el potencial gravitatorio era 0
Buenas, no entendí el primer paso como pasaste de dV a -Edr?