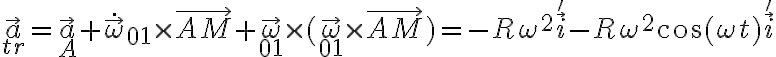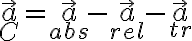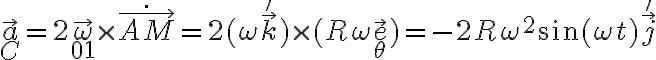Llegue a la aceleración absoluta, pero no se distinguir las aceleraciones de coriolis ni la de transporte, porque por lo que entendí la de coriolis era la centrípeta y si pongo eso me queda en dirección de i' y no me coincide con la solución.
Para llegar a la velocidad y aceleración absoulta derivaste el vector posición directamente o utilizaste los teoremas de Roverbal y Coriolis?
Si bien ambos caminos son correctos, el ejercicio está orientado a ser resuelto mediante la aplicación de los teoremas, ya que las cantidades que se piden hallar son los términos intermedios de aplicarlos.
Otros comentarios que pueden ser útiles:
i) La aceleracion de transporte, coriolis y relativa dependen (además del movimiento de la partícula) del sistema relativo utilizado. A priori ninguna tiene porqué ser la centrípeta ni nada.
ii) Un sistema relativo queda definido por una base de versores + un punto de referencia O' (origen del sist. relativo).
La elección de O' debe ser a consciencia y previa a la aplicación de los teoremas, dado que tiene influencia en los diferentes términos. En tu caso, cuál sistema de referencia elegiste (versores + origen)?
145 palabras
Usando estos versores, pude llegar a la aceleración derivando la posición y luego la velocidad, pero no logro distinguir cual es la aceleración de arrastre, relativa y de coriolis. Tampoco se darme cuenta a partir del dibujo
37 palabras

Hola, Antonella. Tu planteo y cálculos se ven muy bien (tienes cambiado el nombre de los ángulos con respecto a la figura del ejercicio).
Tu pregunta es muy interesante y, en el fondo, hace falta interpretar la letra del ejercicio. Nos pide distinguir las velocidades y aceleraciones de arrastre, relativas y absolutas, "utilizando los sistemas fijo y móvil de la figura".
1) Una primera observación es que en la figura aparecen, de hecho, tres sistemas de referencia.
En realidad hay algunas opciones más, dependiendo de cómo consideremos el origen de cada sistema, pero para fijar ideas elegí O. A y M. Algunos de los vectores en las distintas bases coinciden: 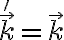 ,
, 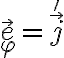 .
.
La respuesta a la pregunta va a depender de cuál de estos sistemas (o sus variantes) vamos a considerar como sistemas fijo y móvil. No parece haber mucha ambigüedad en que la intención del ejercicio es que tomemos  como sistema fijo. En
ese caso, la velocidad y aceleración absolutas son las que tú ya calculaste. ¡Bien!
como sistema fijo. En
ese caso, la velocidad y aceleración absolutas son las que tú ya calculaste. ¡Bien!
Para saber cuál es el sistema móvil al que se refiere el ejercicio, debemos reflexionar en que si consideramos 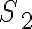 , nos vamos a encontrar con que el punto M está en reposo con respecto a ese sistema. ¿Podrías decir cuanto valen su velocidad y aceleración
relativa en ese caso? No tengas miedo de que la respuesta sea demasiado obvia.
, nos vamos a encontrar con que el punto M está en reposo con respecto a ese sistema. ¿Podrías decir cuanto valen su velocidad y aceleración
relativa en ese caso? No tengas miedo de que la respuesta sea demasiado obvia.
Habiendo determinado (trivialmente) la velocidad relativa de M en 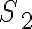 , una forma de proceder es calcular la velocidad de transporte planteando
, una forma de proceder es calcular la velocidad de transporte planteando
y en forma análoga para hallar la aceleración de transporte (¿qué se puede afirmar de la aceleración de Coriolis en este caso?). Para ganar cierta confianza en la interpretación de los resultados, recordemos que
- la velocidad relativa refleja el movimiento del punto con respecto al sistema móvil
- la velocidad de transporte proviene del movimiento del propio sistema móvil: es la velocidad que tienen los puntos que están en reposo relativo en el sistema móvil.
- Ídem para la aceleración relativa y aceleración de transporte.
- la aceleración de Coriolis resulta de la situación de una rotación del sistema móvil junto con una velocidad relativa a éste; por definición este término es perpendicular tanto a la velocidad relativa como a la velocidad angular.
En casos como este no sabría decir cómo usar el dibujo para reconocer cada parte fácilmente; cuando está todo presente es más complicado reconocer cada uno. Así que va a haber que confiar en los cálculos...
2) Luego de haber hecho todo esto, podríamos decir que se podría usar 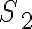 como sistema móvil, pero no tiene mucha gracia (¿cambia en algo cambiamos su origen por A, digamos?). Elijamos entonces
como sistema móvil, pero no tiene mucha gracia (¿cambia en algo cambiamos su origen por A, digamos?). Elijamos entonces 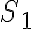 como sistema móvil para contestar el ejercicio.
como sistema móvil para contestar el ejercicio.
Este es el caso que corresponde a la velocidad relativa en tu planteo: 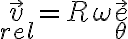 . Lo que está sucediendo al llegar a la aceleración es que para separar las diferentes contribución, los términos parecen confundirse entre
si debido a que aparece la misma velocidad de rotación,
. Lo que está sucediendo al llegar a la aceleración es que para separar las diferentes contribución, los términos parecen confundirse entre
si debido a que aparece la misma velocidad de rotación,  , para
, para 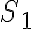 con respecto a
con respecto a  y para
y para 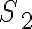 con respecto a
con respecto a 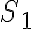 . Es decir, si no fuera el mismo
. Es decir, si no fuera el mismo  en ambos casos, sería más sencillo distinguir los términos de
la aceleración absoluta:
en ambos casos, sería más sencillo distinguir los términos de
la aceleración absoluta:
¿Cómo conviene proceder, entonces? No estoy del todo seguro de cuál es la forma más eficiente, pero más vale ir por un camino seguro. Tratemos de calcular por separado algunas de las varias aceleraciones. La más simple (en principio) parecería
ser la relativa, porque como M realiza un movimiento circular uniforme en 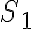 con velocidad angular
con velocidad angular  y radio
y radio  , su aceleración es centrípeta y fácilmente podemos poner (hecho en varios problemas anteriores, o usando la hoja de fórmulas):
, su aceleración es centrípeta y fácilmente podemos poner (hecho en varios problemas anteriores, o usando la hoja de fórmulas):
(el resultado lo escribimos usando la base que nos resulte relativamente más cómoda; la base de 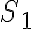 sirve para encontrar el resultado final). Estoy usando
sirve para encontrar el resultado final). Estoy usando 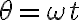 , además.
, además.
Tampoco es muy difícil determinar la aceleración de transporte, ya que la velocidad angular de 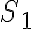 es constante:
es constante:
ya que A, el origen de 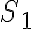 realiza un movimiento circular uniforme de radio
realiza un movimiento circular uniforme de radio  y velocidad angular
y velocidad angular  con respecto a
con respecto a  .
.
En este momento ya tenemos tres de las cuatro aceleraciones. La aceleración de Coriolis se podría calcular a partir de
y además, para verificar usando la definición, calculamos
Una viveza criolla para identificar la aceleración de Coriolis es el factor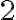 que lleva multiplicando. En este ejercicio sirve, pero no es un método general y puede fallar en ocasiones (¿se imaginan algún caso en que podría fallar
este «brillante» razonamiento?)
que lleva multiplicando. En este ejercicio sirve, pero no es un método general y puede fallar en ocasiones (¿se imaginan algún caso en que podría fallar
este «brillante» razonamiento?) Otra cosa que vale la pena intentar es, provisoriamente, cambiar el nombre de uno de las velocidades de rotación, p.ej.
 en lugar de
en lugar de  , y rastrear a dónde va a parar cada contribución en la aceleración.
, y rastrear a dónde va a parar cada contribución en la aceleración.Espero que se haya entendido. Quedó largo, pero si quedan preguntas, ¡no duden en consultar!
Saludos,
NC
989 palabras

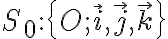
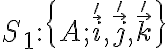
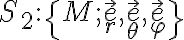

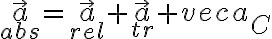
![\vec a_{rel} = -R \omega^2 \vec e_r = -R \omega^2 [\cos(\omega t) \vec i' + \sin (\omega t) \vec k'] \vec a_{rel} = -R \omega^2 \vec e_r = -R \omega^2 [\cos(\omega t) \vec i' + \sin (\omega t) \vec k']](https://eva.fing.edu.uy/filter/tex/pix.php/fc465cbc50cdef976d3c8961ed29337d.gif)