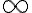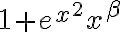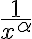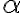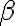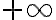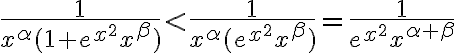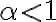Buenas, estaría necesitando ayuda para entender el ejercicio, cuando resuelvo me queda una armónica de cero a infinito, pues (1+ex^2x^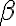
) tiende a 1 con x tendiendo a 0, lo cual diverge para todo alpha, claramente me estoy equivocando pero no se en que, agradezco la ayuda.
Gracias.
Hola Lautaro. Creo que nos conviene pensar la integral en dos partes. Digamos de 0 a 1 y de 1 a 
.
Para la parte de 0 a 1 tenemos, como bien decís, que el factor 
tiende a 1 y la convergencia está determinada por el comportamiento de 
. Para la región de integración que estamos considerando, es convergente si 
, independientemente de 
.
Para la parte de 1 a 
tenemos que 
. Lo cual converge independientemente de 
y por orden de exponenciales.
Juntando ambas condiciones te queda que converge sii 