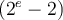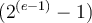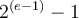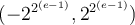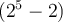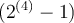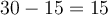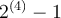Hola, mi duda refiere a que en las notas existe una forma de representar el infinito. Eso implica que el rango de representacion de punto flotante son todos los reales?
O si me preguntan el rango de representación de punto flotante, ¿tengo que poner el ultimo valor antes de la convención de infinito?
ej todos 1 en exponente menos el ultimo que sea 0, y todos 1 la mantisa, variando el signo tengo el mas negativo y el mas positivo.
Gracias
En respuesta a Gianluca Giordano Pignatta
Re: Rango de representacion de punto flotante
de Gustavo Brown -
Gianluca,
Cuando pedimos el rango nos referimos al menor número (finito) representable y al mayor número (finito) representable.
En el caso de punto flotante con N bits para el exponente y M bits para la manitsa es el número cuyo exponente codificado es (2^N)-2, y cuya mantisa es (2^M)-1 y luego con el signo obtenes el menor y el mayor. O sea lo que dijiste al final es correcto.
Ahí obtenes el mayor y menor número codificado, tenes que decodificarlo para indicar qué números son.
Saludos,
Gustavo
En respuesta a Gustavo Brown
Re: Rango de representacion de punto flotante
Buenas,
Siendo n = total de bits y e = bits del expontente, entonces es correcto que el rango de representación es el intervalo [-(2^n -2^e -2), 2^n -2^e -2] ?
Muchas gracias
Siendo n = total de bits y e = bits del expontente, entonces es correcto que el rango de representación es el intervalo [-(2^n -2^e -2), 2^n -2^e -2] ?
Muchas gracias
En respuesta a Maria Soledad Techera Gomez
Re: Rango de representacion de punto flotante
de Gustavo Brown -
No, tenes que interpretar el número [1 | 111...110 |111...111] y el número [0 | 111...110 |111...111] (números de igual magnitud y signo opuesto)
Si tenes e bits de exponente, el desplazamiento es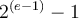
Si tenes e bits de exponente, el desplazamiento es
El mayor exponente codificado es 
Decodificamos el exponente para obtener el real: E 
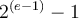
El número está normalizado y la mantissa son todos 1, asi que es 1,111....1 (en base 2) que es casi 2.
Así que el rango queda 
Por ejemplo, para los números de precisión media (1 bit de signo, 5 de exponente y 10 de mantissa) tenemos que
E 
y como estos números están normalizados y multiplicados por 1,1111111111 (en base dos) por lo tanto el rango queda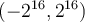 
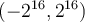
Saludos,
Gustavo
En respuesta a Gustavo Brown
Re: Rango de representacion de punto flotante
Hola, viendo esta respuesta me surge una duda, ¿por qué el mayor exponente codificado es 2^e -2 y no 2^e-1? Después entiendo el resto de las cuentas, pero me surge una duda, si e es la cantidad de bits del exponente, si estoy en media precisión e=5 verdad? Entonces el rango quedaría (-2^4,2^4). Esto no me coincide con la solución al parcial de 2013 que dice que el rango es (-2^16,2^16). Adjunto foto.
Espero respuesta, muchas gracias.
Espero respuesta, muchas gracias.
En respuesta a Lucia Thais De Oliveira Gude
Re: Rango de representacion de punto flotante
de Gustavo Brown -
Pasa que las cuentas que había puesto eran para el exponente. El numero en punto flotante (normalizado) es (-1)^s*1,mantissa*2^exponente
Entonces en el rango faltaba poner el 2^. Ahora acomodé el rango y puse el ejemplo para precisión media, y da como resultado lo mismo que la solución del parcial de 2013.
Entonces en el rango faltaba poner el 2^. Ahora acomodé el rango y puse el ejemplo para precisión media, y da como resultado lo mismo que la solución del parcial de 2013.
Lo de 2^e-2 es porque el caso en que el exponente tiene todos 1 está reservado para indicar infinito (cuando la mantissa tiene todos 0) y NaN (not a number, cuando la mantissa es distinta de 0)
Saludos,
Gustavo