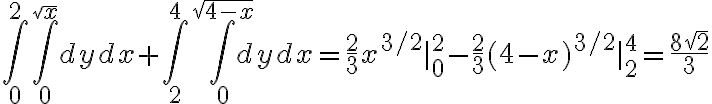Integre en 2 partes, cuando la x va de 0 a 2 y de 2 a 4, el resultado me dio 0, en la solucion dice que es (16√2)/3 y queria saber si ese resultado es correcto, muchas gracias.
Fijate que te piden el área de un conjunto, así que a no ser que ese conjunto tenga interior vacio, el área va a ser positiva.
Seguro te equivocaste en algún signo y se te eliminaron cosas.
El área esa la podes ver como el doble de la siguiente suma de integrales (es simétrica respecto al eje x)
Por que en la primera la y se mueve entre 0 y √x? a mi me quedo al reves, entre √x y 0. Y en la segunda la y me quedo que se mueve entre 2 y √4-x
Pude resolverlo, muchas gracias!