Hola Fabrizio. Pensemos en qué necesitamos para el teorema de Bolzano en una variable y cómo se adaptaría:
En una variable necesitabamos una función contínua en un cierto intervalo cerrado ![[a, b] [a, b]](https://eva.fing.edu.uy/filter/tex/pix.php/022022f289db140169cd9514f74ee648.gif) de modo que
de modo que 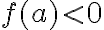 y
y 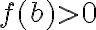 (o viceversa). Como consecuencia, el teorema nos garantiza la existencia de al menos una raíz.
(o viceversa). Como consecuencia, el teorema nos garantiza la existencia de al menos una raíz.
Esto nos llevaría a pensar en algo así como "si tengo una función 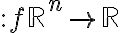 contínua, un valor con imagen posiitiva y otro con imagen negativa... ¿me basta para garantizar la existencia de una raíz?". Lo importante para garantizar eso es emular la hipótesis del intervalo cerrado, para lo cual pediremos que la función sea continua no solo en
contínua, un valor con imagen posiitiva y otro con imagen negativa... ¿me basta para garantizar la existencia de una raíz?". Lo importante para garantizar eso es emular la hipótesis del intervalo cerrado, para lo cual pediremos que la función sea continua no solo en  y en
y en  sino también en una misma bola abierta que contenga a dichos puntos (si estuviéramos en una variable, pensá que pedimos continuidad en un intervalo abierto que contenga a
sino también en una misma bola abierta que contenga a dichos puntos (si estuviéramos en una variable, pensá que pedimos continuidad en un intervalo abierto que contenga a ![[a,b] [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) , es pedir incluso un poco más que las hipótesis de Bolzano).
, es pedir incluso un poco más que las hipótesis de Bolzano).
Si eso se cumple, podés garantizar que habrá una raíz. Y para demostrarlo podes apelar a Bolzano en una variable, construyendote una función auxiliar ![\alpha: [0,1] \mathbb{R}^n \alpha: [0,1] \mathbb{R}^n](https://eva.fing.edu.uy/filter/tex/pix.php/0c702a10e30c19cc32bc2afa8ec089d6.gif) que construye el segmento
que construye el segmento 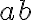 , es decir,
, es decir,  .
.
Cosas interesantes de esta construcción:
la composición ![f \circ \alpha: [0,1] \rightarrow \mathbb{R} f \circ \alpha: [0,1] \rightarrow \mathbb{R}](https://eva.fing.edu.uy/filter/tex/pix.php/317384673a80d4cd466457c4c4d4bc78.gif) es una función en una variable (aunque en el medio pasen otras cosas), por lo que, si verifica las hipótesis, estaríamos en condiciones de usar Bolzano (el clásico, digamos).
es una función en una variable (aunque en el medio pasen otras cosas), por lo que, si verifica las hipótesis, estaríamos en condiciones de usar Bolzano (el clásico, digamos).
En caso de que aplique Bolzano, la existencia de raíces de dicha composición implica la existencia de raíces de  .
.
Pedir continuidad en la bola abierta fue una forma un poco grotesca de asegurarme de que sea continua en el segmento que une  y
y  . Se podría relajar esa hipótesis pero la idea es esencialmente la misma.
. Se podría relajar esa hipótesis pero la idea es esencialmente la misma.
Saludos
