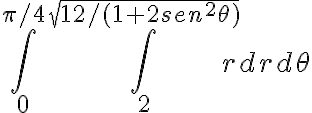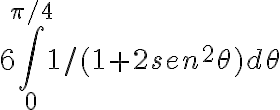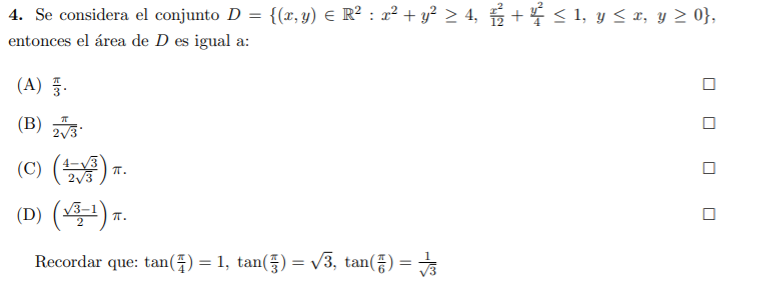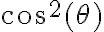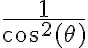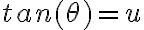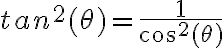Foro de Ejercicios fuera de los Prácticos

Buenas, no se como calcular una integral de este ejercicio.

Hice el cambio a polares, y el dominio me quedó lo siguiente:

$D= \theta \in[0, \pi/4 ], r \in [2, \sqrt{12/(1+2sen^2 \theta )} ]$

Entonces la integral que intenté calcular fue:

$\int_{0}^{ \pi/4 }{ \int_{2}^{ \sqrt{12/(1+2sen^2 \theta )} }{rdrd \theta } }$

La integral de "adentro" la pude resolver sin mucho problema, y cuando la evalué, la separé en dos partes, la parte que me esta generando problemas para calcularle la integral, es:

$6\int_{0}^{ \pi/4 }{1/(1+2sen^2 \theta) d \theta }$

Intenté con varias cosas, entre ellas un cambio de variable, pero no logro llegar a nada en concreto, quisiera saber si la idea del ejercicio es resolverlo por este método, o si hay un camino mas fácil y no me di cuenta.

Gracias, saludos.

Adjunto el ejercicio.