No logro llegar al resultado de ninguna de las dos derivadas de segundo orden en (0,0). Estoy intentando hacerlo usando el límite de la función auxiliar sobre h^2, pero me da distinto. Quizá estoy fallando en alguna hipótesis utilizando esto, algún consejo que me puedan dar?
Considerando que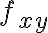 
es la derivada parcial (respecto de 
) de 
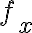, te conviene primero hallar la función 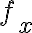en gral. Esto es, derivando la expresión correspondiente para el caso 
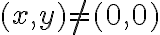y usando la definición para 
.
Una vez obtenida dicha función, podés hallar su derivada parcial respecto a en usando la definición.
Lo mismo, pero derivando en el orden inverso, para hallar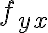 
.
Saludos
Ahora si logré llegar, muchas gracias. Saludos