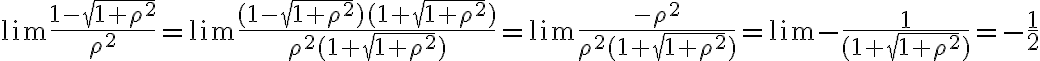Hola, el problema es el último paso
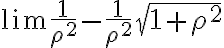 no es cierto que da cero. Me gustaría saber por qué pensaste que daba cero, o mejor dicho, que dijeras que propiedad estas usando, como para ver que efectivamente no es válido. Lo que tenes es una indeterminación
no es cierto que da cero. Me gustaría saber por qué pensaste que daba cero, o mejor dicho, que dijeras que propiedad estas usando, como para ver que efectivamente no es válido. Lo que tenes es una indeterminación  digamos. La forma que se me ocurre de resolverlo es:
digamos. La forma que se me ocurre de resolverlo es: