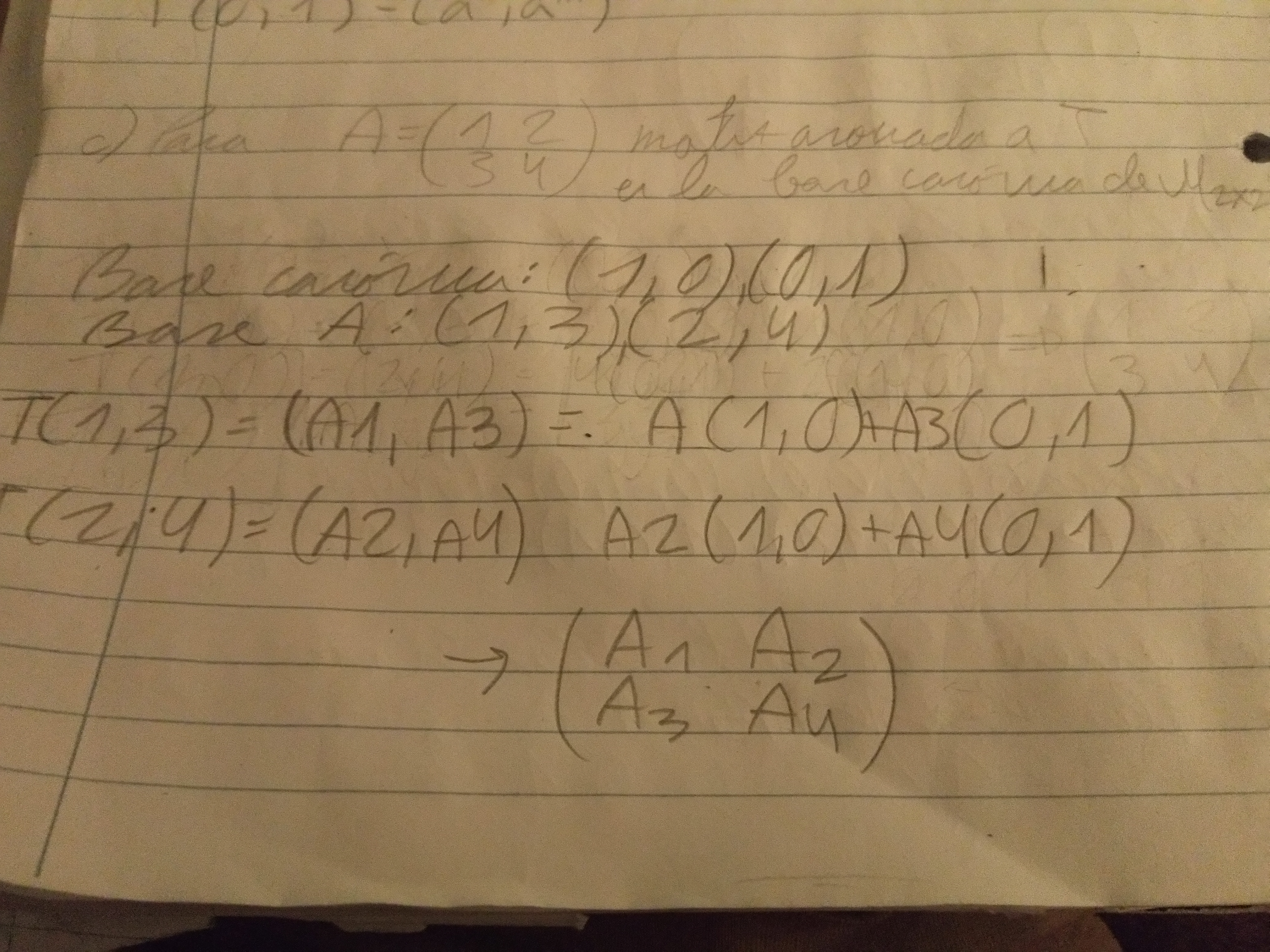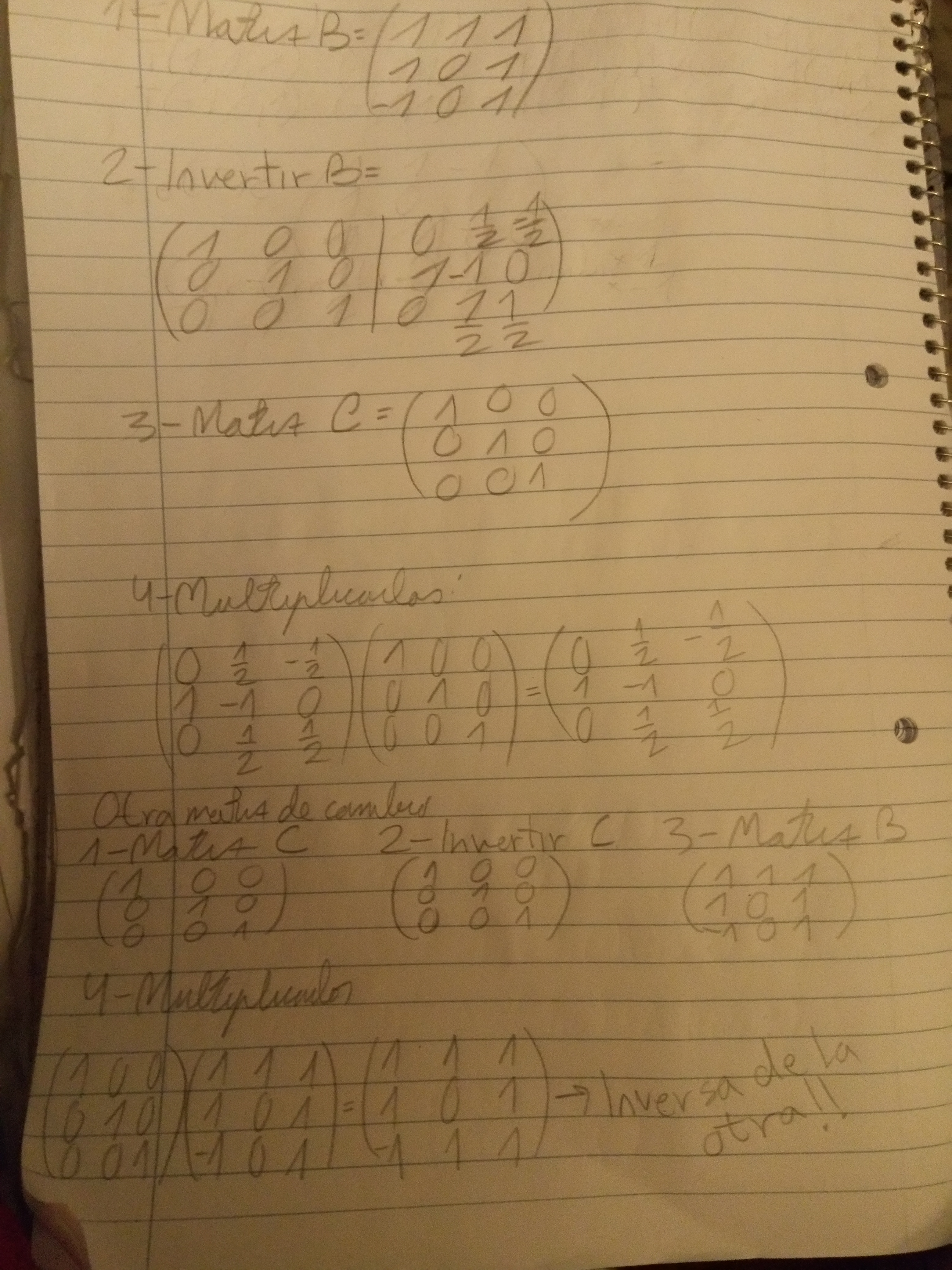Algunos ejercicios del práctico y algunas preguntas

Algunos ejercicios del práctico y algunas preguntas

de Nataly Melanie Ruber Maimo -
Número de respuestas: 5

Hola profe, este práctico está algo complicado así que tengo algunas dudas 

En la 1.1.c., me pasa que entiendo el procedimiento para la solución pero no entiendo la letra de ese ejercicio, o sea, capto de forma general lo que quiere decir pero no sé si tal vez se me podría explicar un poco lo que plantea?

La parte 2 me costó un montón pero después de ver cómo se hacen sólo tengo duda de las últimas dos, la parte de), yo había intentado separar en casos e intentar hacer dos matrices del estilo a,b,c,d, una que cumpliera con ser invertible y otra que no, pero no me salió, y vi la respuesta y no capto lo que hizo el profe, él tomó dos matrices, una de vectores (1,0)(1,0) y otra de vectores (0,0)(0,1) y luego aplicó que típicamente se hace de ver qué pasa en la suma y eso, pero no capto bien qué hizo y por qué, pongo foto por si no se entendió


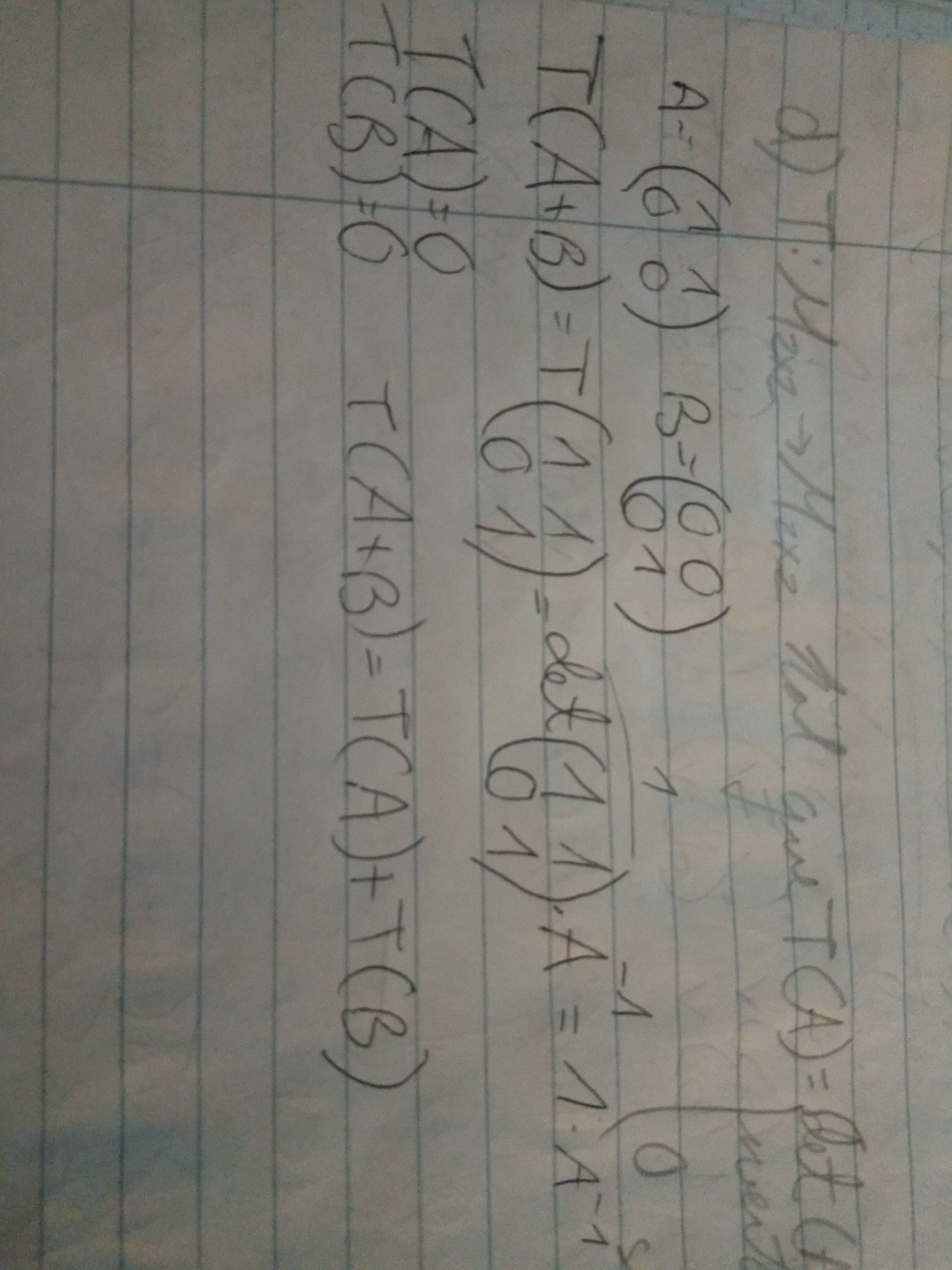
En la e) me pasa que tampoco entendí la forma de solucionarlo, yo había intentado hacer algo como Te(kv+u) y así pero fue mala idea, pero la solución no la capto mucho


No sé bien para qué tomo un w, y todo lo demás ya se me hace algo confuso

En la 3, T está bien definida, porque tiene preimágenes propias de R² no? Yo lo vi así, como que es por eso, o sea si Te fuera tipo Y=(1,2,3,4) ahí ya no estaría bien definido en R², luego para hallar T(p), lo correcto es, como piden algo general, escribir ax²,bx,c, ese sería p, y como piden para todo p, refiere a que consiga todos los a ,b y c que se pueden hallar usando bases de T, así que como ahi tengo esos 3 vectores, hago a(1,0)+b(1,1)+c(0,0), que me va a dar, (a+b, b) ,es este el razonamiento correcto? O al menos el que aplicar para cuando me pidan hallar algo parecido


En la 4, a), no sé 100% si lo que hice es del todo correcto 


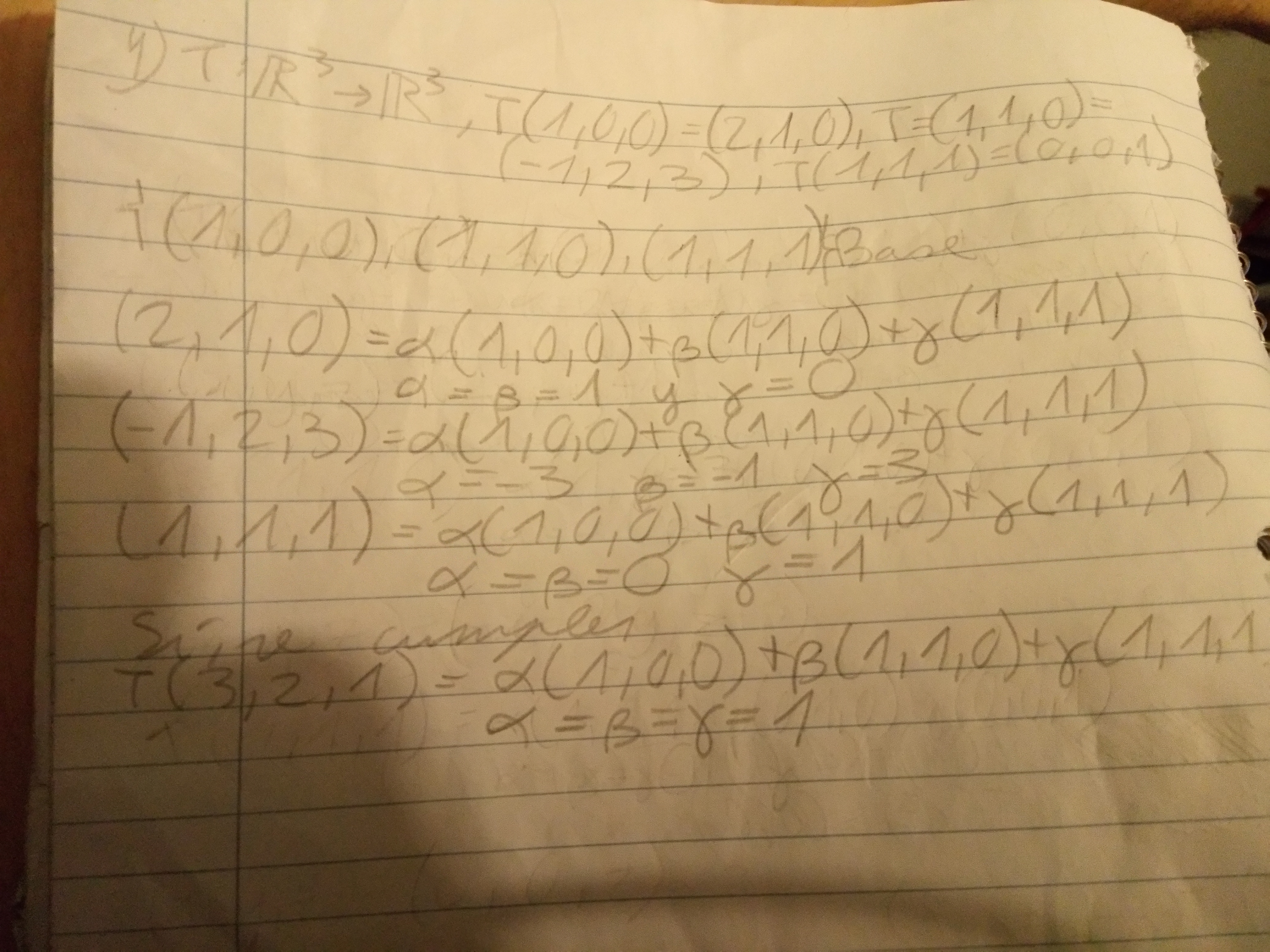
Luego en la 5) hallar la forma general pero para matrices se me hizo algo complejo, pero noto que es algo simple, sólo que se me da mal, hice esto:


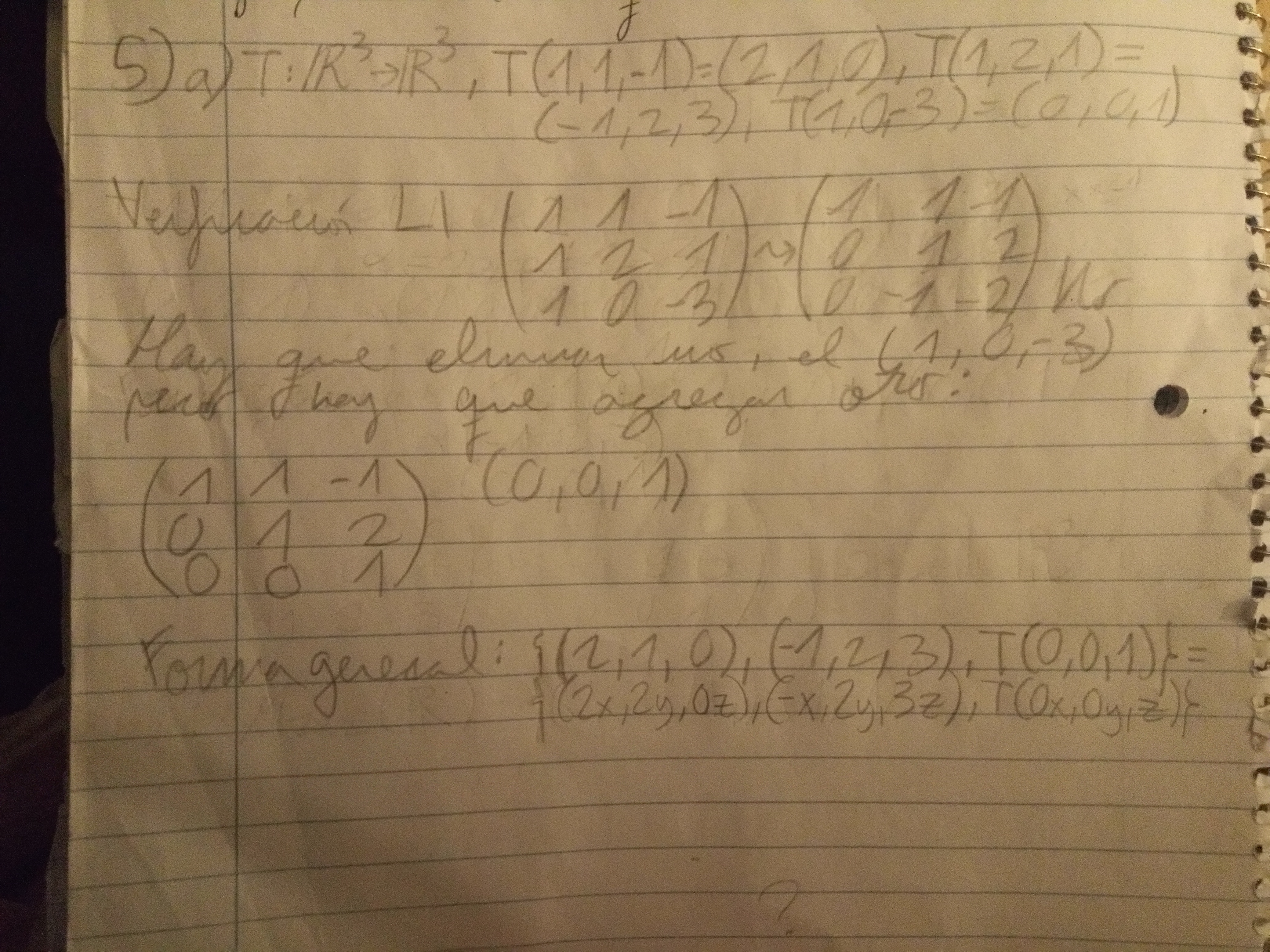
En este ejercicio 5) tengo algunas dudas, por ejemplo, el profe se "salteó" la verificación de LI, y le pregunté a alguien y me dijo que no hace falta, pero esto de acá ni siquiera es LI, hay que meterle otro vector para que siga de R³, eso no influye en el ejercicio?  Yo le puse el vector (0,0,1), y la forma general, no sé del todo si se anota así en vector, de todas formas probablemente esté mal

En la 5b sin embargo sí fue necesario hacer la verificación, hasta el profe la hizo, e incluso eliminamos vectores para que además quedara algo propio de R², ese ejercicio creo que me quedó claro


En la parte 2, la parte a me quedó así, no se si la correcta, porque son números algo feos


Y en la parte b), no sería como buscar (x²+x-1) pero con +1 en vez de -1? Se me ocurre el mismo procedimiento pero cambiando ese signo, pero no sé si cuenta como expresión general

Finalmente, quería ver si esta demostración estaba bien, porque es de lo que más me cuesta 

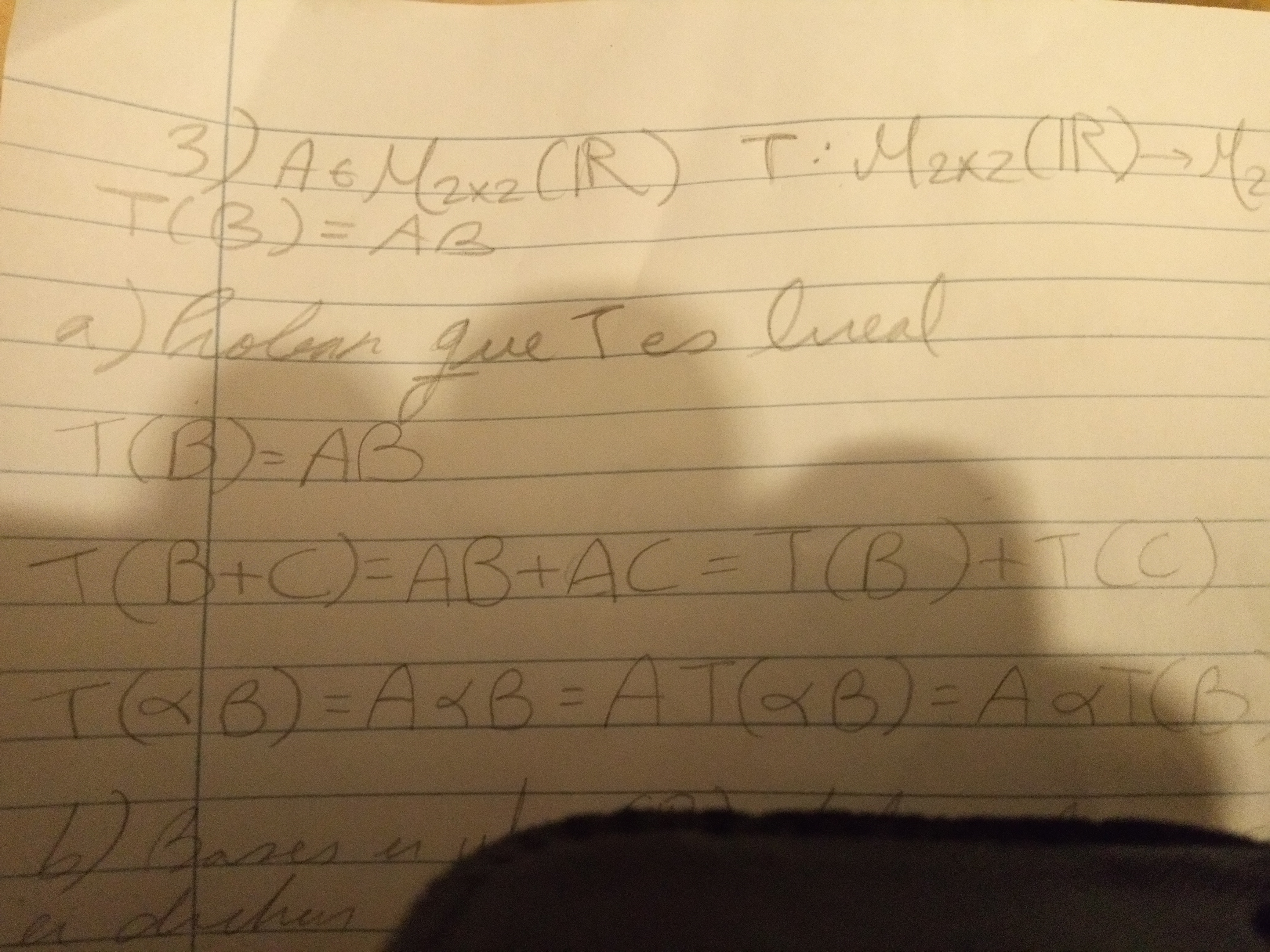
En la parte de la suma, pensé que como T(B) lleva a AB, entonces T(C) debería llevar a AC, y el resto lo normal


Todavía me falta practicar más las matrices asociadas ,así que por ahora no tengo preguntas de ello, pero gracias por contestar !! 

En respuesta a Nataly Melanie Ruber Maimo

Re: Algunos ejercicios del práctico y algunas preguntas

de Nataly Melanie Ruber Maimo -

Buenas al final practiqué cambio de base y lo que restaba y conseguí el resto, a ver si salió bien!

Las únicas donde me costaron un poco fueron las 3)b y c, pero capaz llegué a algo: en la b), yo creo que sí hay una base, lo pensé así,

Debe haber un T(a)=A y un T(a')=A, en realidad que cada uno sea "la mitad" de A, por así decirlo, y entonces pensé, puede ser la identidad, T(1,0) y T(0,1), porque eso, si yo lo analizo en una base de A, me da A en total me parece, por ejemplo si A fuese hecho de los vectores (a,a'),(a'',a'''), y que ella sean su base, es cosa de elegir esos como los T(1,0) y T(0,1) ,así lo pensé

En el c


Capaz está mal cómo evalué A en T, pero mi idea era que siT(B)=AB, entonces T de cualquier cosa tendrá a A multiplicando por la izquierda, capaz no debí suponerlo para todos los casos ?

Luego, el 4 no fue problema, y el 5 creo que tampoco, pero como el 5 parece importante, te muestro a ver qué te parece


Yo entendí que cuando decía "otra matriz de cambio de base" se refería a hacer cambio de base pero para el otro lado, o sea de delante para atrás, y ahí se comprobó que queda inversa 



Graciasssssss

Perdón por molestar tantoo

En respuesta a Nataly Melanie Ruber Maimo

Re: Algunos ejercicios del práctico y algunas preguntas

de Bruno Dominguez -
Hola Nataly,

El 1.1.c te plantea una transformación que va desde el espacio de las funciones que son continuas entre 0 y 1 a los reales, tal que el transformado de una función f es la función evaluada en 0 $$(T(f)=f(0))$$.


En el 2d se planteó un contrajemplo para mostrar que es falso. Lo que hizo fue mostrar que la linealidad no funciona para esa T que se plantea. Como A y B no son invertibles T(A)=T(B)=O y T(A)+T(B)=O, pero $$A+B=\left( \begin{smallmatrix}1&1\\0& 1 \end{smallmatrix}\right) $$si es invertible $$det(A+B)=1$$ y $$(A+B)^{-1}=\left( \begin{smallmatrix}1&-1\\0& 1 \end{smallmatrix}\right)$$, por lo tanto $$T(A+B)=\left( \begin{smallmatrix}1&-1\\0& 1 \end{smallmatrix}\right) \neq \left( \begin{smallmatrix}0&0\\0& 0 \end{smallmatrix}\right)=T(A)+T(B)$$.


En el 2e, la idea es correcta pero creo que te mareas al plantearlo. Por un lado tenés que $$v=\alpha_1v_1 + ... \alpha_n v_n$$ y $$w=\beta_1v_1+...+\beta_nv_n$$, o sea que $$coord_B(v)=(\alpha_1,...,\alpha_n)$$ y $$coord_B(w)=(\beta_1,...,\beta_n)$$. Por otro lado tenés que $$\mu v+\lambda w=\mu (alpha_1 v_1 + ... \alpha_n v_n)+\lambda (\beta_1 v_1+...+\beta_n v_n)=(\mu \alpha_1+\lambda \beta_1)v_1+...+(\mu \alpha_n+\lambda \beta_n)v_n$$,
o sea que $$coord_B(\mu v+\lambda w)=(\mu \alpha_1+\lambda \beta_1,...,\mu \alpha_n+\lambda \beta_n)=\mu coord_B(v)+\lambda coord_B(w)$$. Por lo tanto la linealidad se cumple.


Para los 3, 4 y 5 te recomiendo que leas este post: https://eva.fing.edu.uy/mod/forum/discuss.php?d=186442

En el 3, T está bien definida xq conoces los transformados de una base del espacio de salida. Luego lo de cómo hallar T(p) está explicado de forma un poco confusa pero el resultado es correcto.

En el 4 no entendí qué quisiste hacer, para probar qué única es con lo de conocer los transformados de la base. Y al final T(3,2,1) no lo hallaste.

En el 5,OJO! Al eliminar vectores para hacer al conjunto LI tenés que eliminar columnas no filas, son las columnas las representan a los vectores. En este ejercicio no tenés que agregar vectores. Ahora sobre tus preguntas, en realidad siempre tendrías que chequear si es LI o no. Lo que decis que "para que además quedara algo propio de R²" no se bien a qué te referís, pero el espacio de llegada para ver cuántas transformaciones existen no te importa mucho.

Leete el post que te puse más arriba a ver si con eso queda más claro como proceder, cualquier cosa volvé a preguntar.


En el 2.2.a primero te diría que revisaras las cuentas. Luego por lo que entendí que querías hacer, vos hallaste los transformados de la base del espacio de salida pero después no entendí, si lo querés hacer por ese lado tendrías que ver cómo escribir tu vector $$(x^2+x-1)$$ en función de tu base para recién ahí aplicar la transformación usando linealidad.

Otra forma de hacer este ejercicio es con la fórmula: $$_B(T)_Acoord_A(v)=coord_B(T(v))$$, entonces con las coordenadas de tu vector que querés hallar su transformado multiplicas la matriz asociada por eso y te da las coordenadas del transformado en el espacio de llegada, ahí "desarmas" las coordenadas y obtenés T(v).

En la parte b sería lo mismo pero con $$ax^2+bx+c$$ en vez de $$x^2+x-1$$, xq querés hallar el transformado de un vector genérico.


Del 3a, casi bien, la última línea te quedaría $$T(\alpha B)=A \alpha B = \alpha AB=\alpha T(B)$$.

Del 3b en realidad no, te dejo este post: https://eva.fing.edu.uy/mod/forum/discuss.php?d=186820

Del 3c, OJO! La base canónica de $$\mathcal{M}_{2\times 2}$$ no es $$\{(1,0),(0,1)\}$$, sino que es: $$\left \{ \left( \begin{smallmatrix}1&0\\0& 0 \end{smallmatrix}\right) , \left( \begin{smallmatrix}0&1\\0& 0 \end{smallmatrix}\right) , \left( \begin{smallmatrix}0&0\\1& 0 \end{smallmatrix}\right) , \left( \begin{smallmatrix}0&0\\0& 1 \end{smallmatrix}\right) \right \} $$, fijate que lo que vos pusiste son vectores y no matrices, y A no es una base, es una matriz!

Para el primer caso lo que tendrías que hacer es: $$T \left( \begin{smallmatrix}1&0\\0& 0 \end{smallmatrix}\right)=\left( \begin{smallmatrix}1&2\\3& 4 \end{smallmatrix}\right) \left( \begin{smallmatrix}1&0\\0& 0 \end{smallmatrix}\right) $$ el resultado de ese producto sería el primer transformado, luego tenés que pasarlo a coordenadas y hacer lo mismo para las otras tres matrices.


Del 5, acordate que para "pasar" los vectores a matriz estos van colgados no acostados. Lo que planteaste no está bien, la idea de la matriz cambio de base es la matriz asociada a la transformación identidad $$(I:V \to V / I(v)=v)$$, es decir cómo escribir una base en función de la otra. La matriz cambio de base entre B y C $$(_C(I)_B)$$ es fácil de hacer xq como la base de "llegada"" es la canónica, las coordenadas de los vectores de B en C son los mismos vectores de B, por lo que $$_C(I)_B$$ simplemente sería colgar los vectores de B. La otra matriz cambio de base posible es la que va de C a B $$(_B(I)_C)$$, para este vas a tener que hacer algunas cuentas, serían las coordenadas de los vectores de la base canónica en la base B.

Ahora el tema de que una es inversa de la otra. Dadas dos transformaciones $$T:V \to W$$ y $$S:W \to U$$ y la composición $$SoT:V \to U$$ y A,B y D bases de V,W y U respectivamente se tiene que \( _D(SoT)_A =_D(S)_B. _B(T)_A \). Ahora, pensado $$T:V \to W$$ invertible $$(T^{-1}:W \to V)$$, se tiene que $$ToT^{-1}=I$$, entonces $$_A(ToT^{-1})_A=_A(T)_B._B(T^{-1})_A=_A(I)_A=I_n \implies _B(T^{-1})_A = (_A(T)_B)^{-1}$$. Tomando $$T=I$$ te queda xq una matriz cambio de base es inversa de la otra. Con esta propiedad podés chequear si hiciste las cuentas bien (en este caso te lo pide el ejercicio igual), si hiciste las cosas el producto de las dos matrices cambio de base te tiene que dar la matriz identidad.


Bueno, fueron varias cosas, cualquier cosa preguntá de nuevo.

Saludos!
En respuesta a Bruno Dominguez

Re: Algunos ejercicios del práctico y algunas preguntas

de Nataly Melanie Ruber Maimo -
Ok, sólo me quedaron algunas pocas cosas en el aire; en la 4, ya capté el procedimiento para ver si hay una transformación que cumpla o no, y en el caso de encontrar a T(3,2,1), puedo simplemente, ya que sé que ese T(3,2,1)=T(1,0,0)+T(1,1,0)+T(1,1,1), decir que T(3,2,1)=(2,1,0)+(-1,2,3)+(0,0,1)=(1,3,4), no? leveo sentido pero capaz me equivoco


Luego, en la 5, ya capté a lo que te referías y noté que cuando yo sacaba a esos tres T(M) se me iban columnas y no filas, así que me fijaré en éso siempre, me quedó la duda de si está realmente bien poner que la forma general es (x,-y),(x,y), si es así la respuesta sería infinitas no? pues se pueden poner números en las x e y infinitos

Tengo un tema con la 3c, con la matriz asociada, creo que no me quedó del todo claro, pero a ver si funciona así: para calcular la matriz asociada, necesito dos bases que son las que me dan, entonces tengo que agarrar cada vector de la primer base y aplicarlos en la fórmula de algún T por ejemplo, pero aquí no tengo fórmula, sólo sé que T(B)=AB, entonces, lo que hago es agarro la otra base y escribo lo de alfa(vector)+beta(vector)+gamma(vector), con vector siendo vector de la segunda base, y luego lo paso a vector y éso me da resultado una columna. Lo que me confunde es que en este ejercicio, yo agarro como primer base a la canónica, lo cual se me hace un poco raro, y después hago producto, en vez de usar alfa ni nada (?)

tengo una pregunta también, en la 5, de la parte 2,ahora sí vi cómo se hace la matriz cambio de base, pero tengo una duda, en la 2,1, o sea lo primero de la parte 2, el profe lo que hace es, por ejemplo T(1,0,0)=3(1,0)+1(0,1), o sea agarra el 1,0,0 y lo evalúa en la función, y lo que le de lo escribe en base a la otra base, pero en el caso de la 5, sólo hay que escribir por ejemplo (1,0,0)=a(1,1,1)+b(1,0,1)+c(-1,0,1), obvio no hay una función donde evaluar por así decirlo, pero en la del profe él no hace por ejemplo T(1,0,0)=a(1,0)+b(0,1), T(1,0,0)=(a,b), y a ello una matriz? supongo que no tiene sentido hacerlo porque en el caso de la 2, 1, ya tenés la función para evaluar y eso es tu a y tu b, y en esta tenía que conseguirlos. No sé si estoy diciendo muchas incoherencias, estuve todo el día con gal y capaz ya se me están mezclando las cosas :(

Luego, tengo un problema gordo con el 2.2.a, además probé hacer un ejercicio de parcial que pedía lo mismo y me pasa igual, me cuestan esos (los del estilo hallar T(algo)), tengo un tema con la fórmula y es que no me sale, la intento seguir pero no hay forma, no sé si me puedas ayudar con éso porque lo vi en el teórico y no le agarro la mano, capaz me serviría un ejemplo, porque lo de desarmar tampoco termina de encajarme, trataré de escribir un posible procedimiento, ver si el procedimiento es algo así (con ese mismo ejercicio); usando la fórmula, primero el b(T)a ya lo tengo y se llama u(T)epsilon, la coordenada en a(v), es la coordenada en épsilon de mi v a calcular, así quedaría algo como: u(T)epsion por coordepsilon(v), y éso es igual a coord u (T(v)), del v que quiero calcular. Así que primero podría hacer el producto de lo que tengo a la izquierda de la igualdad, el v lo escribo como un vector vertical de 3x1, no veo otra forma de que quede bien, así que luego de éso, me queda una matriz 3x3 de vectores (2x2,x2,x2), (2x,3x,2x) y (-1, -1, -2). y eso es la coord u (T(v)), pero quiero T(v), creo que podría descomponer esa matriz, usando el propio u, cosa que me quede (2x2,x2,x2)=a(1,1,0)+b(1,2,3)+c(3,2,1),luego lo mismo con (2x,3x,2x) y (-1, -1, -2), y ta después hacer las cuentas y ahí me quedó una matriz con tres vectores:(2x2, 3x2/4, -1x2/4), (2x, 3x/4, -1x/4) y (-3, 1/2, 1/2). Ese podría ser v, pero a mí se me da bastante mal darme cuenta de estas cosas, así que no sé, qué te parece?

gracias por responderr

En respuesta a Nataly Melanie Ruber Maimo

Re: Algunos ejercicios del práctico y algunas preguntas

de Bruno Dominguez -

Hola,

En el 4, efectivamente por linealidad de las transformaciones lineales T(3,2,1) da eso.


En el 5, como te quedan menos condiciones que la dim del espacio de salida y compatibles entonces te queda que hay infinitas transformaciones si. Ahora, si quisieras hallar la forma general de esas infinitas transformaciones tendrías que agregar a la base un vector genérico (que cumpla que no se CL con los demás) con un transformado genérico y a partir de ahí hacer las cuentas, es decir agregar una condición que sea: $$T(a,b,c)= (\alpha,\beta)$$ de forma que $$a,b,c$$ veriquen que $$ \{ (a,b,c) , (1,1,-1) , (1,2,1) \} $$ sea LI, con esto para cada $$a,b,c, \alpha , \beta $$ distinto va a haber una transformación distinta y por eso son infinitas. No entendí cómo llegaste a tu "forma general".


En el 3c, si te dan la fórmula y esta es $$T(B)=AB$$ con $$A= \left( \begin{smallmatrix}1&2\\3& 4 \end{smallmatrix}\right)$$, es decir los transformados de $$B$$ por $$T$$ son el producto matricial $$AB$$.

Para hallar una matriz asociada $$_B(T)_A$$ vos tenés que agarrar los vectores de $$A$$ transformarlos y hallar las coordenadas de esos transformados en la base $$B$$ (las coordenadas forman un vector). Es decir es agarrar los vectores de $$coord_B(T(A))$$ y colgarlos.

 En este caso tanto tu base de salida y llegada son la canónica de las matrices 2x2. Entonces, primero para cada uno de los vectores canónicos vas a hacer $$T(C_i)=AC_i$$ esto te va a dar otra matriz 2x2 y ahora tendría que hallar las coordenadas de esta matriz en la base de llegada, pero como esta es la canónica, estas coordenadas son las mismas entradas de la matriz, colgas estos vectores y ya te queda.


En el cambio de base, tu función es la identidad $$(I:V \to V/I(v)=v)$$, para $$\mathbb{R}^3$$ sería $$I(x,y,z)=(x,y,z)$$ por eso $$T(1,0,0)=I(1,0,0)=(1,0,0)$$. El tema con el 2.1 es que su base de llegada es la canónica entonces sus coordenadas son los mismos vectores (o sea, lo hace pero saltéandose el paso por así decirlo), pero por ejemplo en el 2.3 ya no es así y tenés que hallarlas con lo del a,b,c que planteas (a,b,c serían las coordenadas del vector en la base de llegada).


Para el 2.2.a, $$v=x^2+x-1$$ y $$\mathcal{E}= \{ 1,x+1,(x+1)^2 \}$$ para hallar las coordenadas de $$v$$ en $$\mathcal{E}$$ tenés que resolver el sistema $$v=x^2+x-1=\alpha1 + \beta x + \gamma (x+1)^2$$ visto de forma matricial te queda $$ \left( \begin{smallmatrix} 1&1&1&|&-1\\0&1&2&|&1\\0&0&1&|&1 \end{smallmatrix}\right) $$, por lo tanto $$coord_\mathcal{E} (x^2+x-1)=(\alpha , \beta , \gamma )=(0,-1,1)$$. Entonces el producto que tenés que resolver es $$ coord_\mathcal{U} (T(x^2+x-1))= \left( \begin{smallmatrix}2&2&1\\ 1&3&1\\ 1&2&2 \end{smallmatrix}\right) \left( \begin{smallmatrix} 0\\ -1\\ 1 \end{smallmatrix} \right) = (a,b,c) $$. Calculado esto solo falta "deshacer" las coordenadas: $$T(x^2+x-1)=a(1,1,0)+b(1,2,3)+c(3,2,1)$$.


Saludos