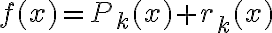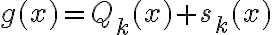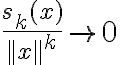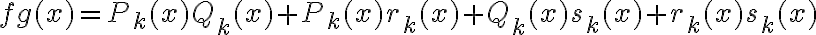Hola! En las clases de openfing el profesor da un ejemplo en el que para la multiplicacion de dos funciones no se puede hacer el polonomio de taylor multiplicando los polinomios de cada una como si fueran de una variable. No me quedó muy claro porque dijo como que en algunos casos si se podía hacerlo, entonces me quede con la duda de cuando se podría hacer de esa manera. Me podrían dar alguna ayuda?
Hola Sol. Para pensar de esa manera hay que tener cuidado con el grado de los polinomios/el orden de infinitésimo del resto.
La clave es recordar que los polinomios de Taylor nos permiten escribir una función  (que cumpla las hipótesis de diferenciabilidad necesarias) como
(que cumpla las hipótesis de diferenciabilidad necesarias) como
donde 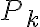 es un polinomio de grado
es un polinomio de grado  y el resto
y el resto 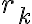 cumple
cumple 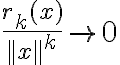 cuando
cuando 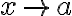 (siendo
(siendo  el punto elegido para desarrollar el Taylor).
el punto elegido para desarrollar el Taylor).
Entonces hay que pensar que pasa cuando la función que quiero desarrollar se escribe como un producto de funciones ¿Puedo usar el polinomio Taylor de cada factor por separado? Con cautela: Si tomamos el polinomio de grado  de cada factor, el polinomio resultante posiblemente tendrá grado mayor a
de cada factor, el polinomio resultante posiblemente tendrá grado mayor a  . Si tomamos grados menores, corremos riesgo de que al polinomio producto le falte algún término respecto del término original.
. Si tomamos grados menores, corremos riesgo de que al polinomio producto le falte algún término respecto del término original.
Una opción es hacer los polinomios de Taylor de grado  de cada factor, multiplicarlos y truncar ese producto (quedándonos solo con la porción del polinomio que es de grado
de cada factor, multiplicarlos y truncar ese producto (quedándonos solo con la porción del polinomio que es de grado  ). O sea, si tengo
). O sea, si tengo  como antes y quiero el Taylor del producto
como antes y quiero el Taylor del producto  con
con
Tendremos
Donde es relativamente fácil probar que si 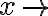 a, los tres últimos términos divididos
a, los tres últimos términos divididos  tenderán a cero. El primer término es el polinomio que decía antes que hay que truncar, y constatar que dicho truncamiento puede hacerse de forma que la parte que descartas también verifique dicho límite (para poder tratarlo como parte del resto, digamos).
tenderán a cero. El primer término es el polinomio que decía antes que hay que truncar, y constatar que dicho truncamiento puede hacerse de forma que la parte que descartas también verifique dicho límite (para poder tratarlo como parte del resto, digamos).
Gracias! Quedo clarísimo