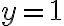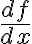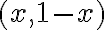Hola, no termino de entender por que en los puntos de la forma (x,1) se puede calcular la derivada parcial y en los de la forma (x,1-x) no se puede, ya que en ambos casos tengo quien es f en los puntos de esa forma. tambien me genera duda de como sabemos que el gradiente de puede calcular en (1,0)? para afirmar eso no tendríamos que saber si es diferenciable en ese punto?
Hola Carolina. El problema en (casi todos) los puntos de la forma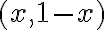 
es que si bien sabés cuanto vale la función en ellos, no sabés cuanto vale la función al moverte un poquitito hacia el costado, o un poquitito hacia arriba (que es lo que hacemos al calcular las derivadas parciales a través de la dirección), por lo que no tenemos información suficiente para hacer el cálculo.
Por otro lado, cuando pide el gradiente en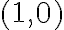 
se refiere simplemente a un vector con las derivadas parciales correspondientes, sin tener en cuenta la diferenciabilidad. Luego, se puede estudiar la diferenciabilidad en ese punto jugando con lo que tendría que cumplir el gradiente si fuese diferenciable vs lo que pasa en realidad.
Saludos
Hola Verónica, a mi me confundió también que pregunte en qué puntos puedo hallar el gradiente, porque entendí que para definirlo la función tenía que ser diferenciable en ese punto. Entiendo que la finalidad de esa pregunta es que observemos en qué intersección de puntos tienen sentido las derivadas parciales en 
y en 
.
Por lo mismo que comentaba Bernardo en otro debate de este foro, no puedo afirmar que la función es diferenciable en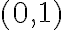
porque si bien es continua en este punto, no sé si esas derivadas existen en un entorno, sino que solo en 3 direcciones.
Agradezco también si es posible me ayuden con la derivada parcial en en los puntos de la forma 
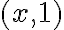con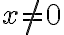 
, porque ese me da 
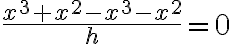, siendo así que 
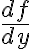existe en 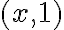además de 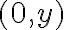en 
.
y en .Por lo mismo que comentaba Bernardo en otro debate de este foro, no puedo afirmar que la función es diferenciable en
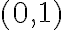porque si bien es continua en este punto, no sé si esas derivadas existen en un entorno, sino que solo en 3 direcciones.Agradezco también si es posible me ayuden con la derivada parcial en
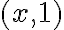en los puntos de la forma con 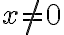, porque ese me da 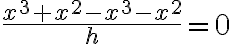, siendo así que 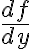existe en 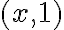además de en 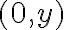.Gracias!
Hola Diego!
La derivada según en el punto con los datos que nos brindan no la podemos hacer, ya que nos dan la función evaluada en 
por lo que no podemos calcular su derivada, dicho de otra forma, no podemos saber cuánto varía según porque ya la tenemos fija.
Saludos!
La derivada según
en el punto con los datos que nos brindan no la podemos hacer, ya que nos dan la función evaluada en por lo que no podemos calcular su derivada, dicho de otra forma, no podemos saber cuánto varía según porque ya la tenemos fija. Saludos!
Aaah tenés razón!
No sé si me confundí al interpretar la letra del ejercicio como una función por partes.
Para confirmar que entendí: tampoco podría calcular
en ni en 
, ¿verdad?
No sé si me confundí al interpretar la letra del ejercicio como una función por partes.
Para confirmar que entendí: tampoco podría calcular
en ni en , ¿verdad?