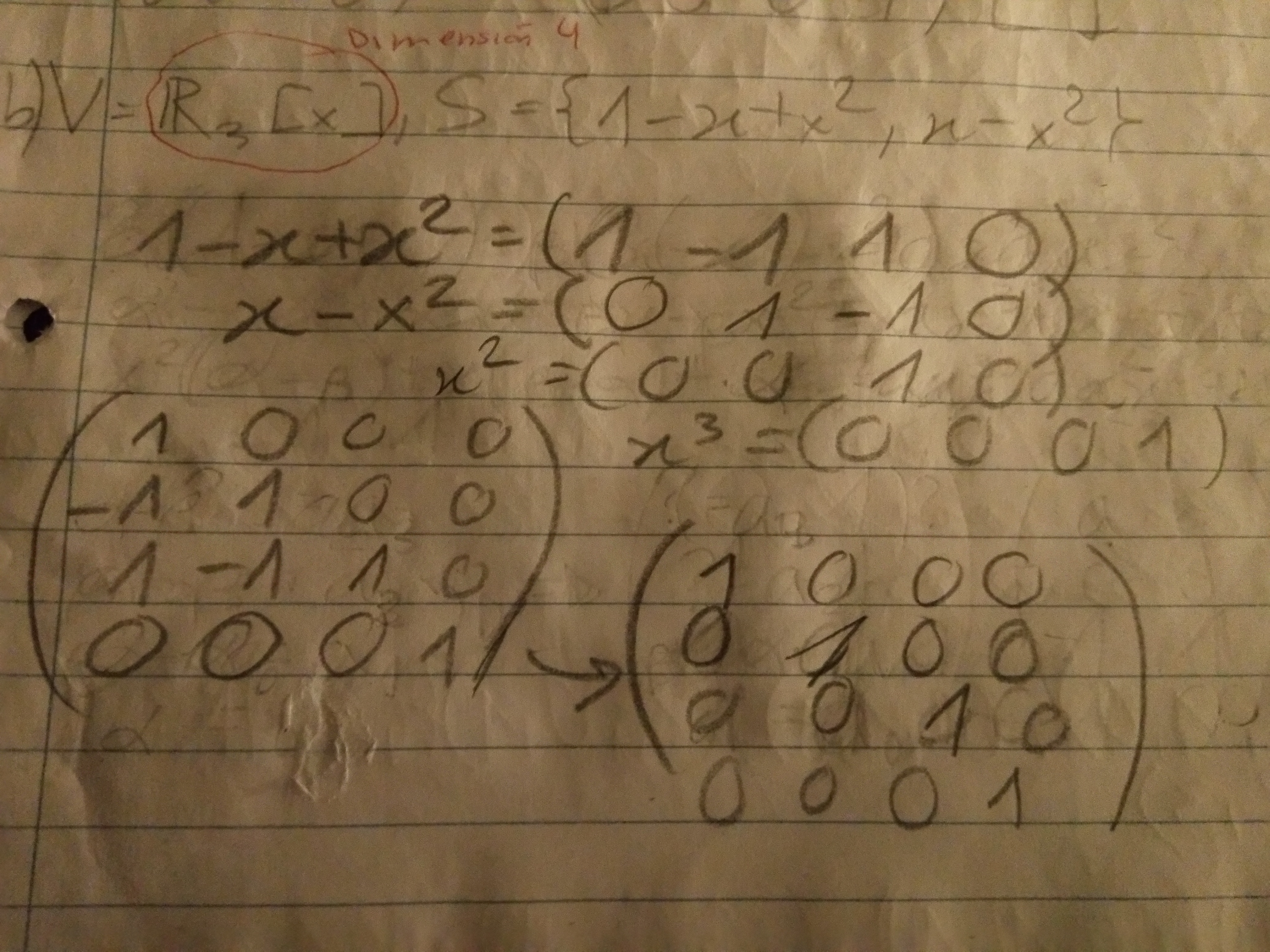Algunos ejercicios de la parte 1

Algunos ejercicios de la parte 1

de Nataly Melanie Ruber Maimo -
Número de respuestas: 6

Hola, hice la parte 1, pero voy a pasar algunos ejercicios para ver si tengo bien los procedimientos


En esta lo que hice fue, hacer la resta de incógnitas y ecuaciones para encontrar los parámetros, así que con 2 parámetros sabía que debía dejarlo en función de dos parámetros, así que por eso puse x=-2b+a, luego ello lo intenté escribir como un generador, por eso a(1,0,1)+b(-2,1,0) y como es LI, es base. La dimensión del subespacio S me parecía ser 2 pues hay dos vectores ,el a(1,0,1)+b(-2,1,0) ,pero no sé 100% si es así porque hay gente que dice que en realidad sería dimensión 3 por ser R³

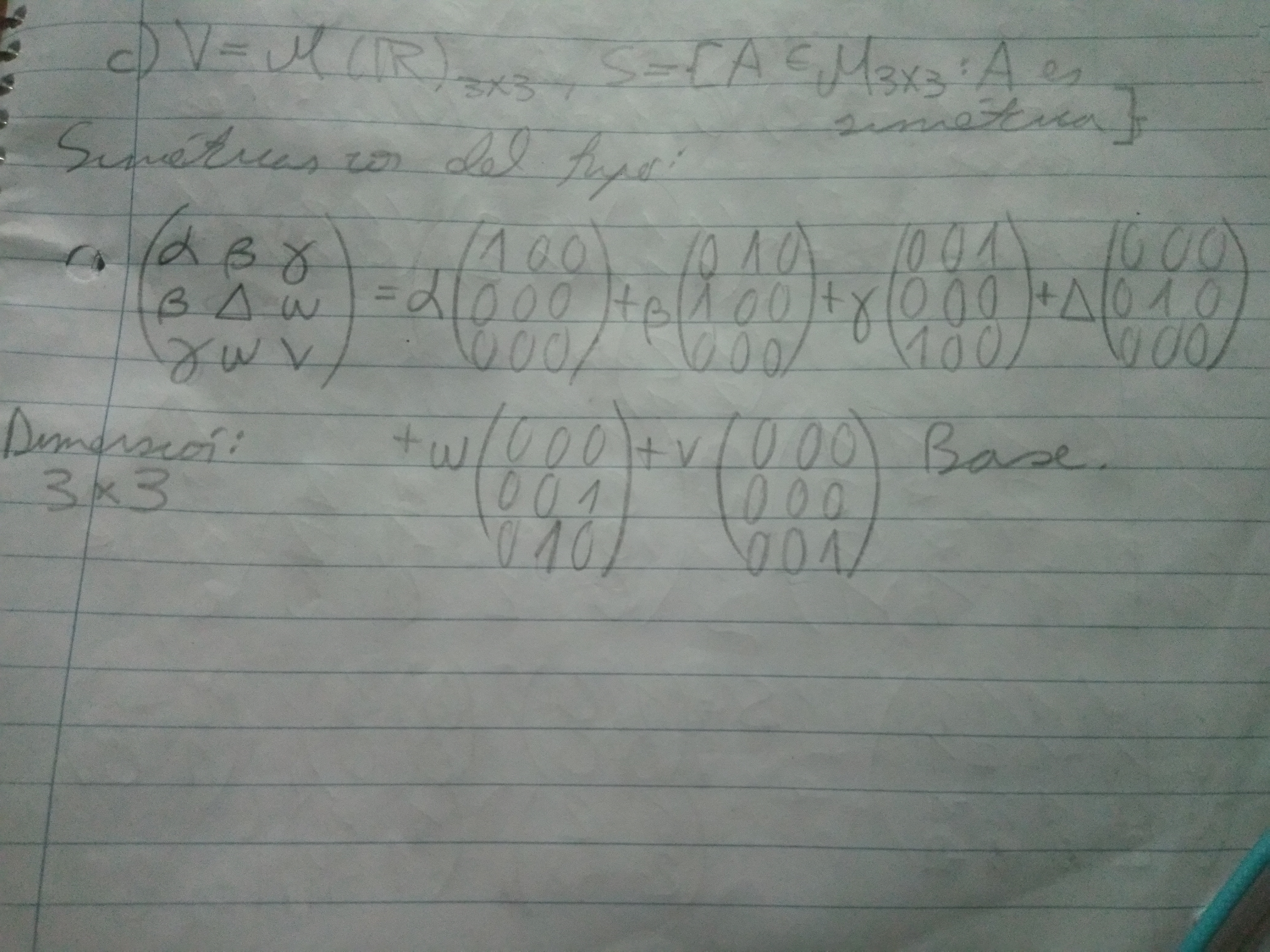 para las matrices es medio parecido creo, pero hallar una base es más fácil parece, la dimensión ahí si sería 3x3, pero tengo una duda, si la dimensión es 3x3 o 2x3, lo que sea, está bien decir que tienen dimensión 9 y 6 respectivamente ? O se queda 3x3 y listo, porque si fuera así una de dimensión 3x2 y otra de 2x3 tendrían la misma dimensión, 6

En el ejercicio d pareciérame que es la matriz nula y que se base está compuesta por ceros, de 2x2


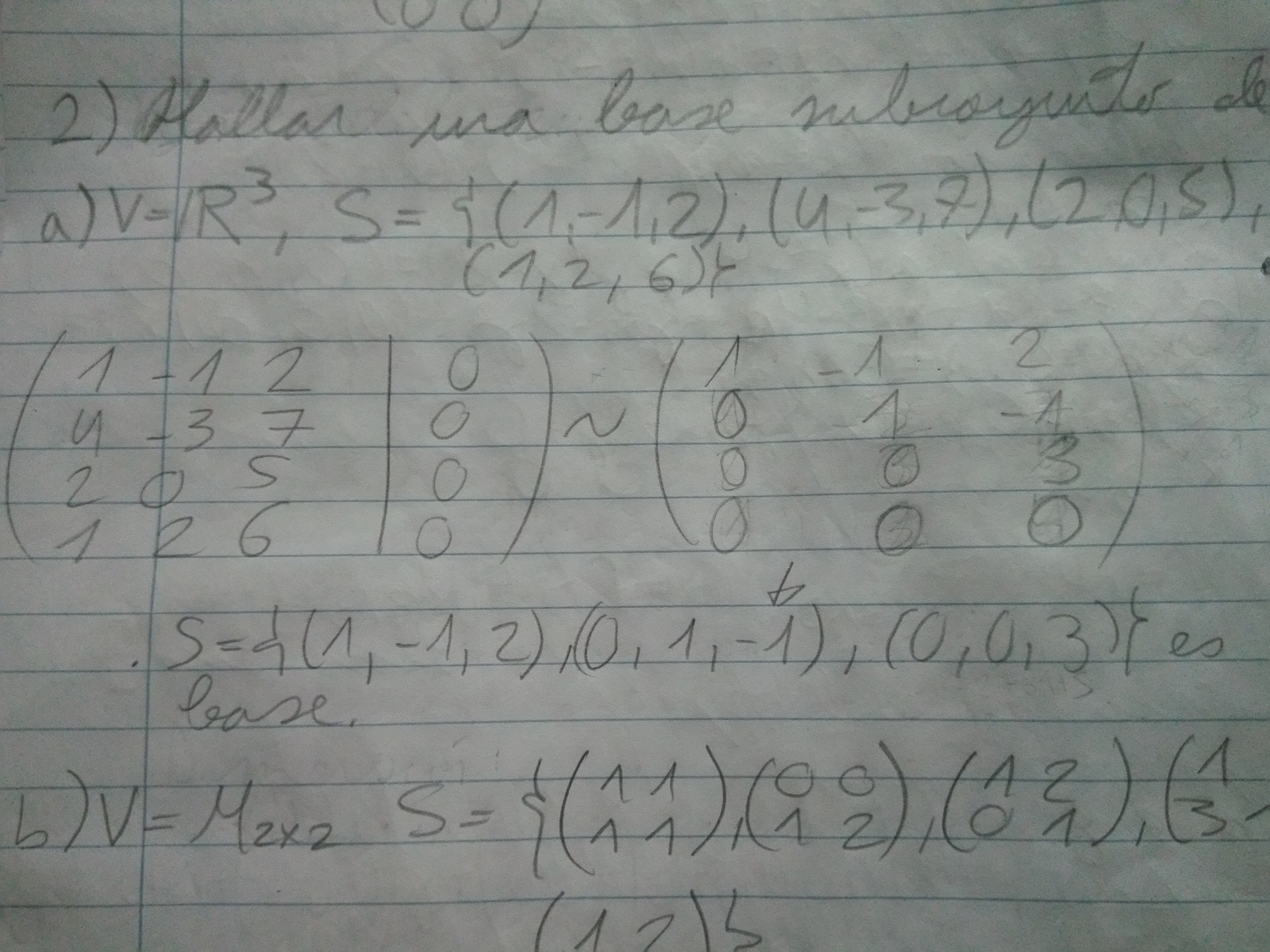
Está correcto anotar las bases así no?  


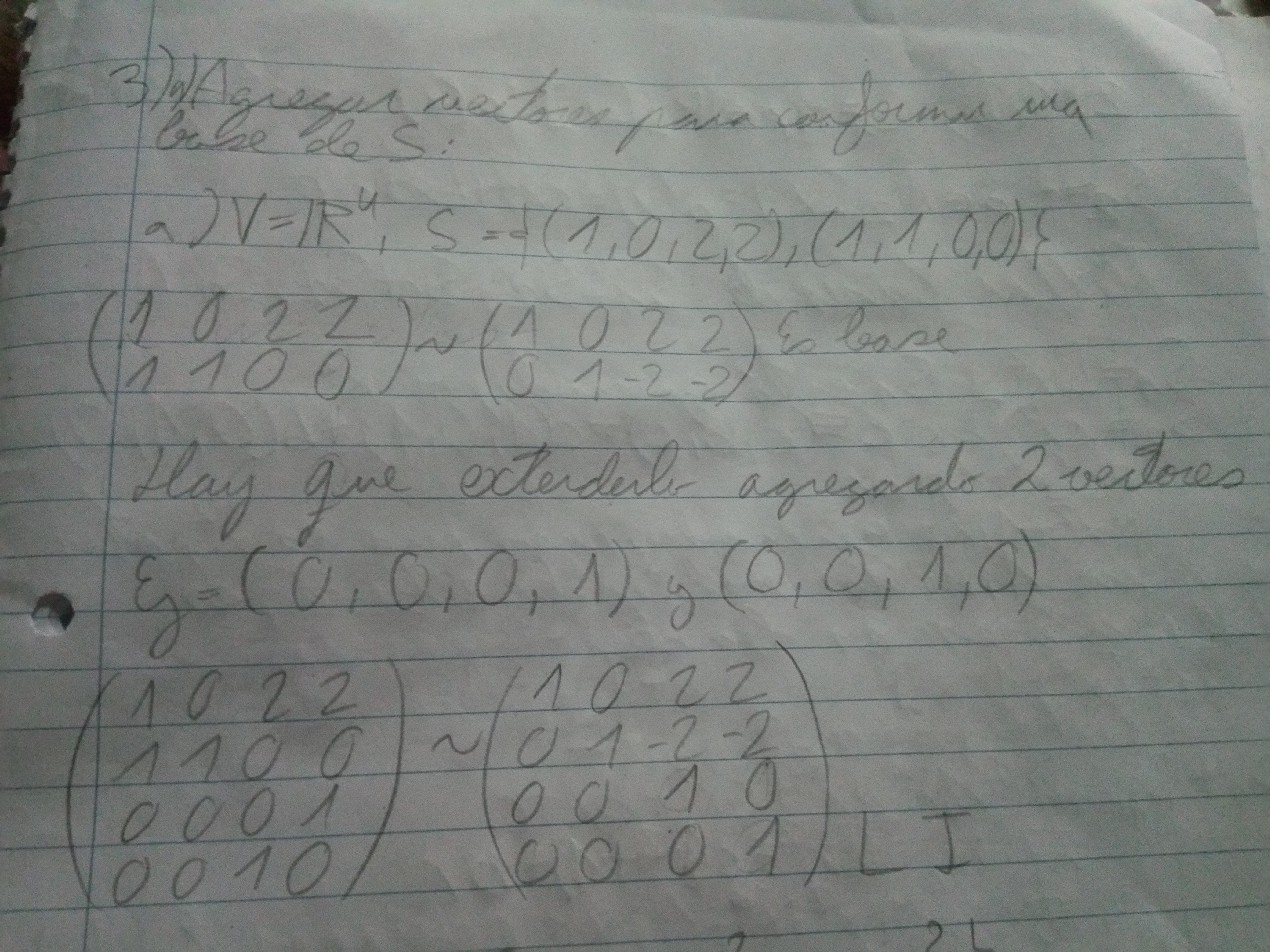
Esta parte de extender para llegar a una base distinta me confundió un poco, porque por ejemplo, este es R⁴, pero entonces necesito 3 vectores? O 4? No termino de captar eso, porque por ejemplo en el anterior que era de R³, me había quedado 2 vectores así que capaz aquí es 3 vectores y no 4 los que necesito


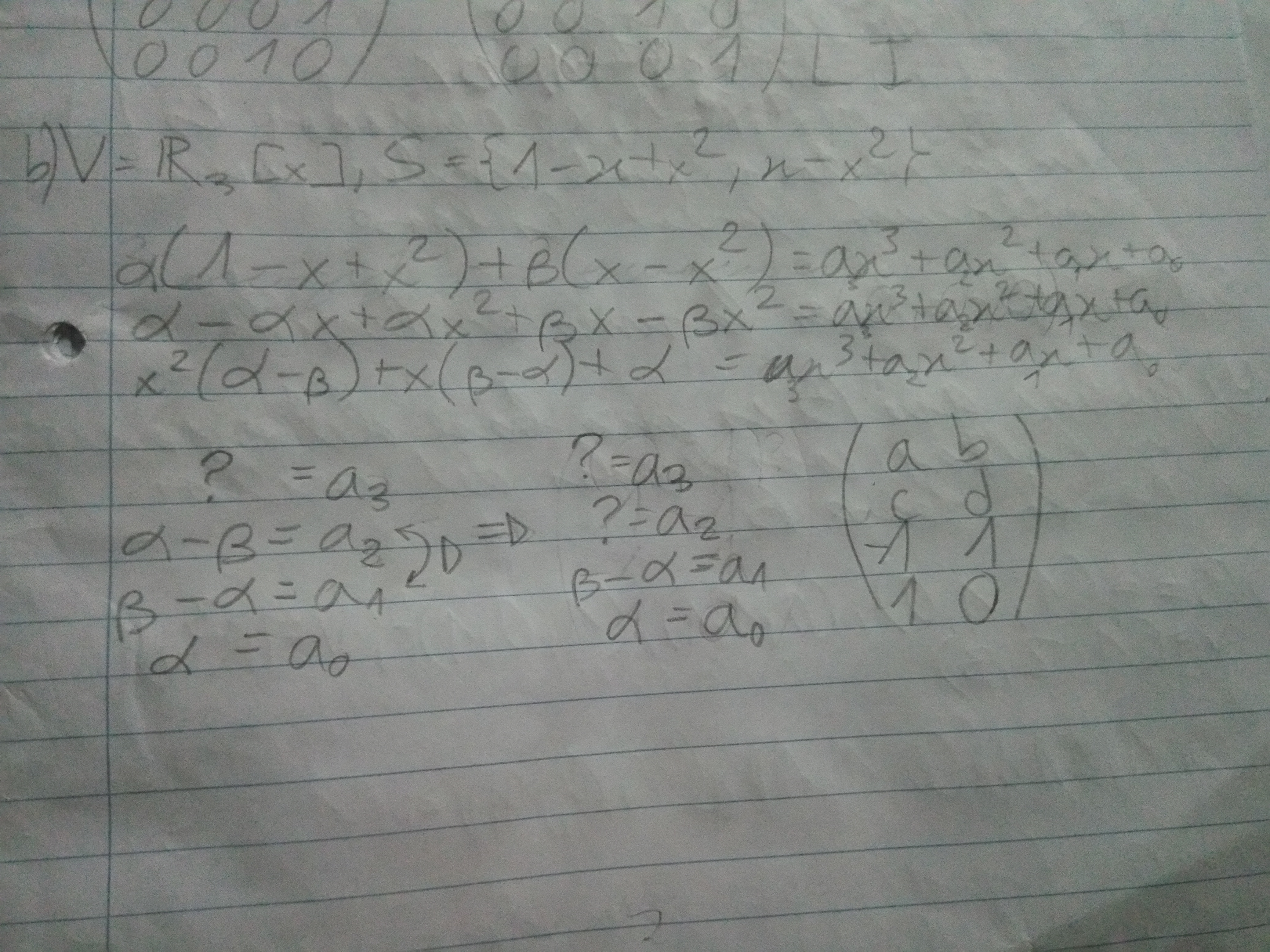
Este también me confundió, intenté hacer el procedimiento de siempre, pero al momento de añadir vectores veo que el a2 y el a1 son dependientes, así que eliminó el a2, pero eso también me queda dependiente, así que añadí uno con la idea de que hubiera elementos hasta a3 pues es de R³, pero no hay manera que quede base así, por lo que hay algo mal.


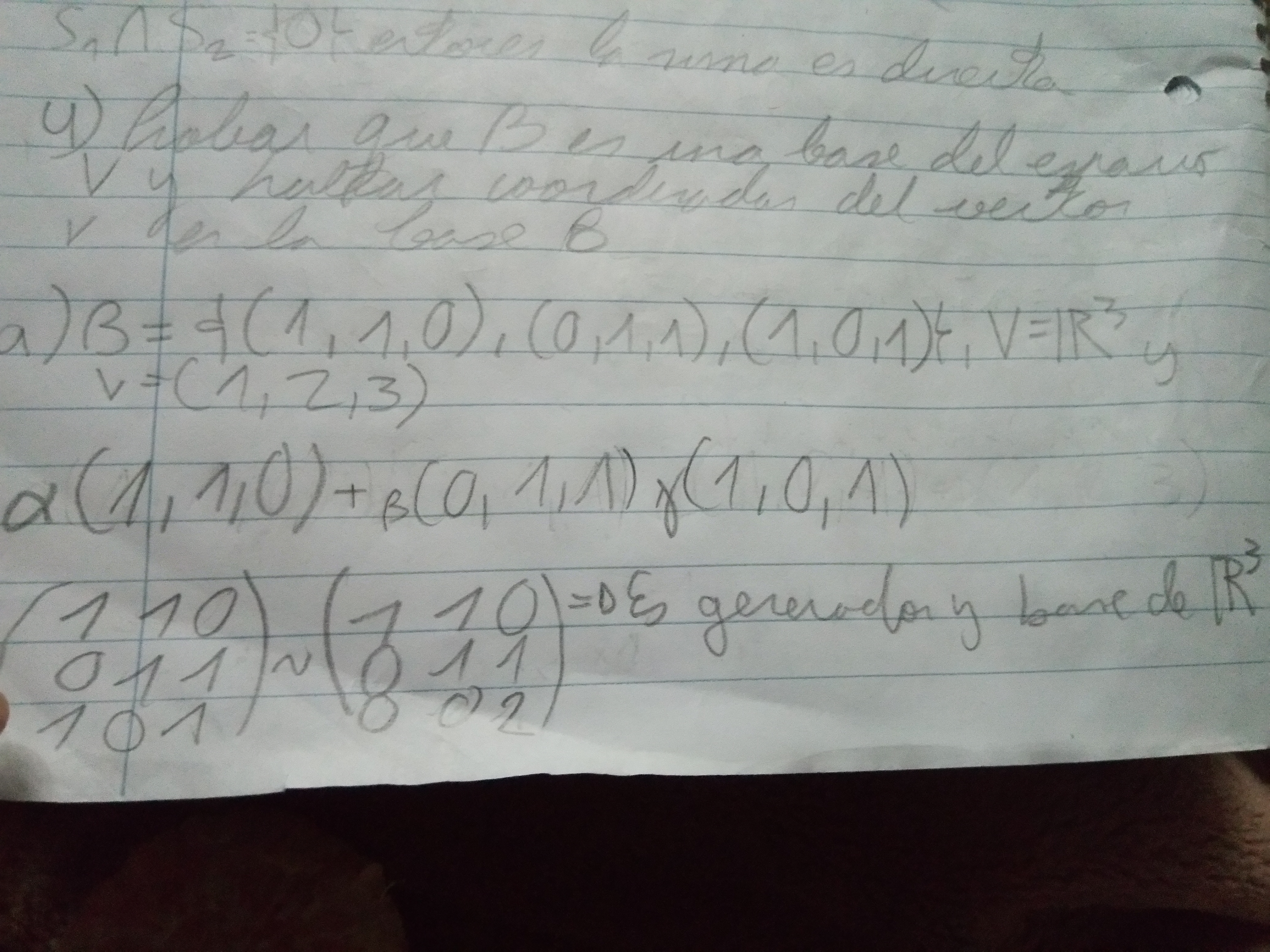
Aquí en este caso, estaría bien que haya 3 vectores de R³? Porque en la primera que pasé quedaba de dimensión 2 y era de R³ también, o sea que capaz sería de R⁴?


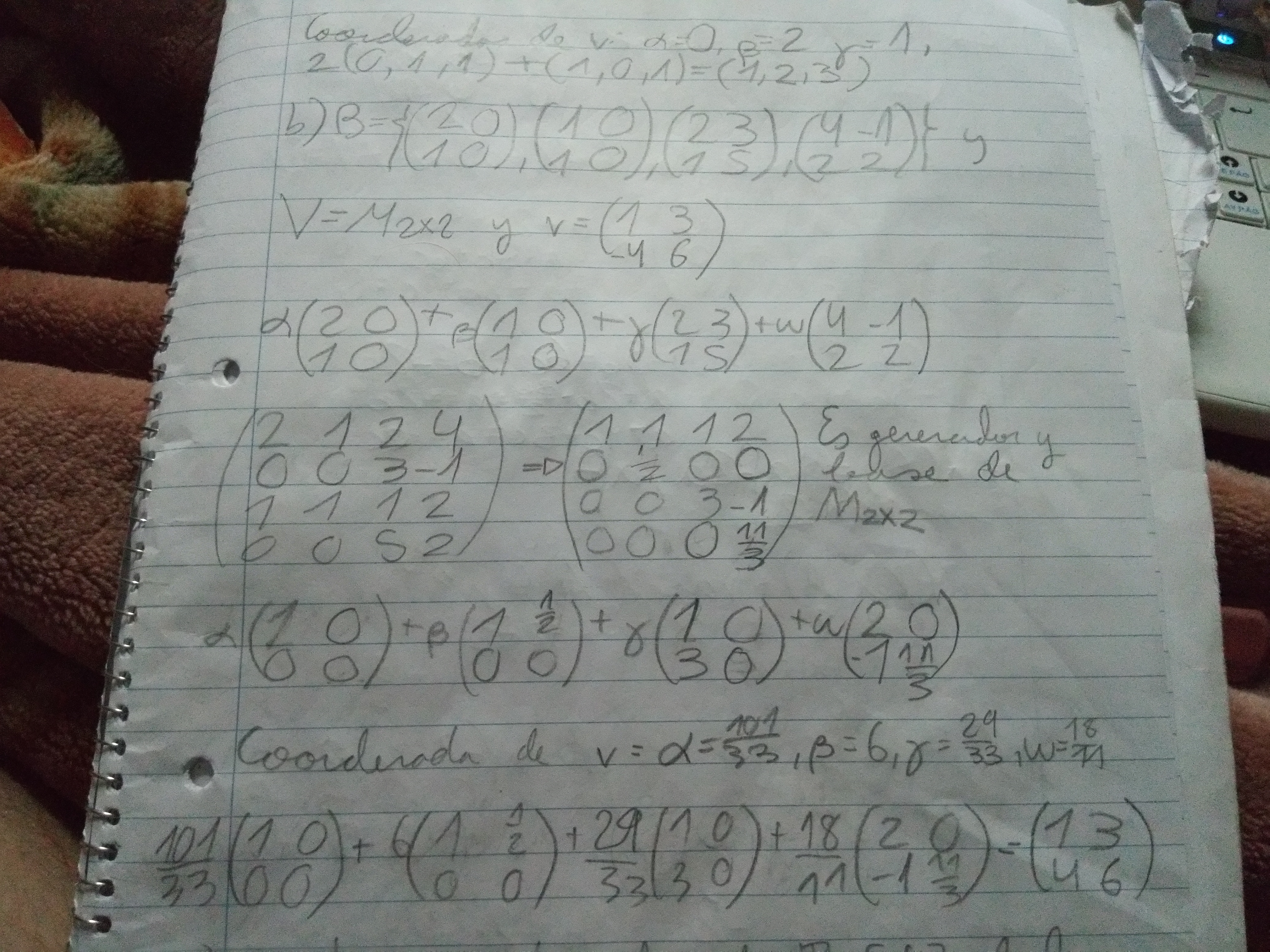
Es así como se busca las coordenadas? Porque me dieron números muy raros, luego no se si las coordenadas se anotan de esa forma, yo lo que busqué son alfas, betas ,omegas y w que produzcan el punto que me dieron, o sea la matriz que me dieron en este caso


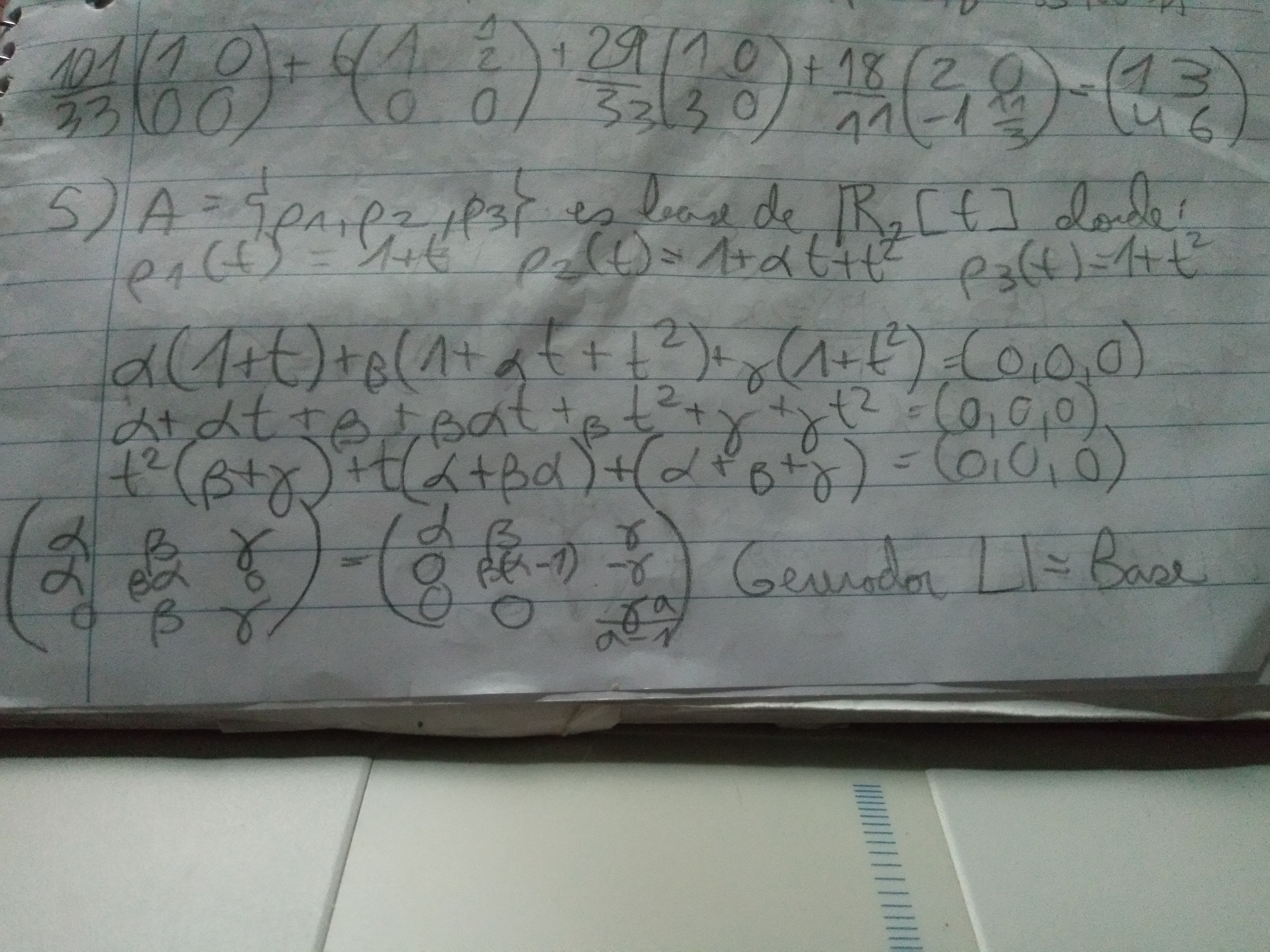
Estos ejercicios me cuestan un poco, pero lo que hice fue intentar juntar los términos de igual grado y hacer una matriz para hallar la base y al parecer existe, sin embargo tengo el mismo problema, y es que tengo 3 vectores aquí, pero es R², así que no sé si estaría bien


Aquí tengo varias dudas, el ker es simplemente los vectores de la matriz del rango no? En los otros ejercicios simplemente agarré la matriz ya trabajada y saqué sus vectores, luego, hay alguna manera de saber la dimensión de el ker sin usar n-rango(A)? Intenté buscar en internet y no me aparecía, sin embargo mi primer idea es que su dimensión debía ser la misma que la del rango, o sea 2x3, pero no daba en la cuenta, no sé si hay una manera de ver que la dimensión es 1 por ejemplo.


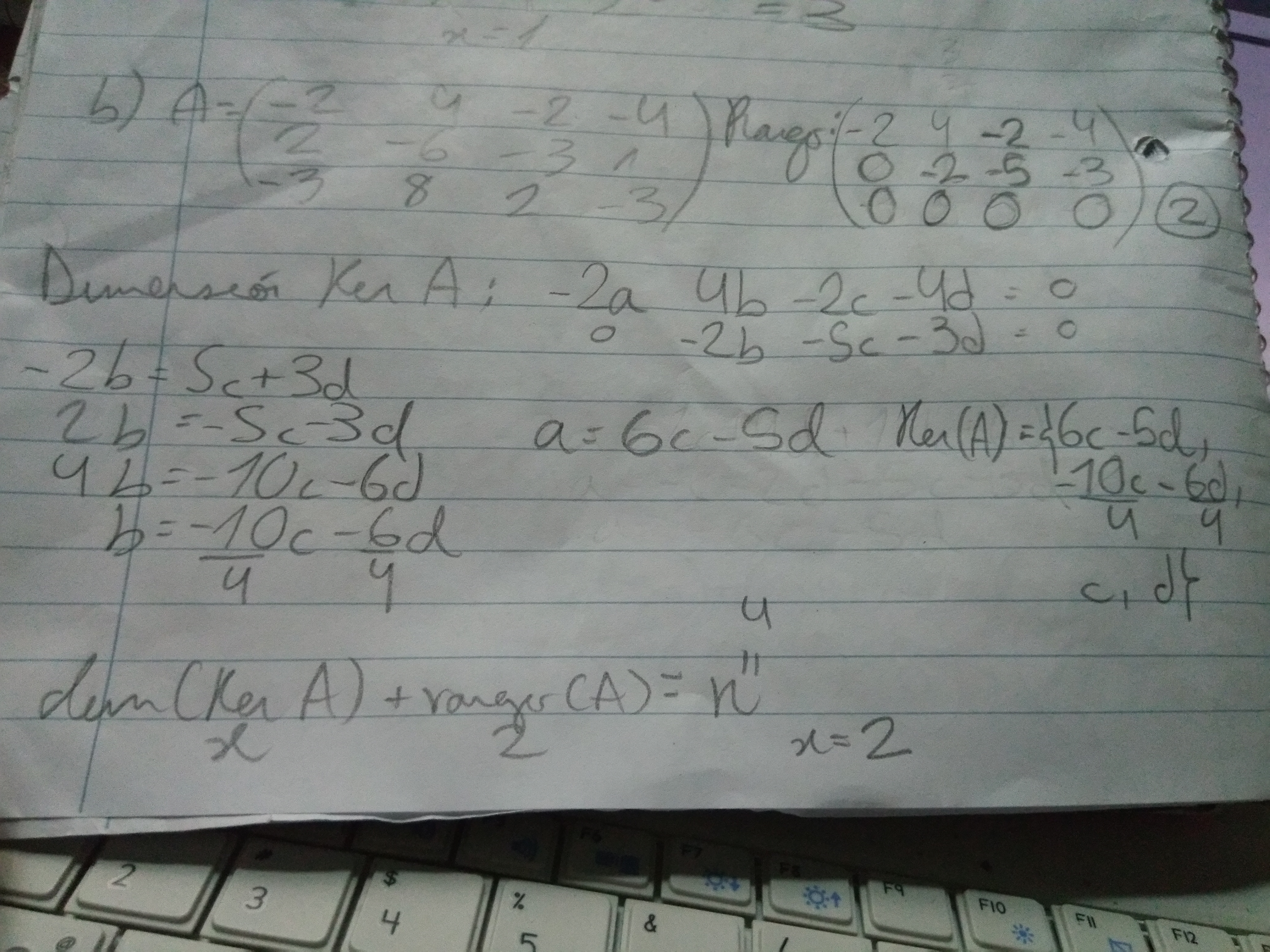
Aquí por ejemplo como ya tenía el rango sólo le puse letras para luego tratar de plantear el ker, pero me quedó medio feo porque no logré escribirlo en función de ninguna letra en particular, de c y d nomás, luego la dimensión la conseguí como la manera anterior, y el otro fue similar al primero



Graciasss eso sería todo por ahora :D

En respuesta a Nataly Melanie Ruber Maimo

Re: Algunos ejercicios de la parte 1

de Martin Eduardo Kenny Pujadas -

Hola Nataly, 

En el ejercicio (1) la idea general es correcta. Acordate que la dimensión de un espacio vectorial coincide con el número de vectores que tiene una base de dicho espacio (si bien existen infinitas bases para un único espacio vectorial, estas siempre tendrán la misma cantidad de vectores), por lo que si bien, por ejemplo en la parte (a), $$\mathbb{R}^3$$ tiene dimensión 3, el ejercicio pide determinar la dimensión del subespacio vectorial S, que como hallaste una base y tiene dos vectores, entonces el subespacio tiene dimensión 2. Luego en la parte (c) ocurre lo mismo, el espacio $$\mathcal{M}_{3x3}$$ tiene dimensión 9, pero el subespacio de las matrices de 3x3 simétricas será de dimensión 6 (ya que la base que hallaste tiene 6 vectores). Revisá la parte (d) que tu planteo no es correcto, te recuerdo que la traza de una matriz es la suma de las entradas pertenencientes a la diagonal de la matriz, por lo que una matriz genérica de dicho subespacio sería de la forma $$\left(\begin{smallmatrix}a&b\\c&-a\end{smallmatrix}\right)$$.

En el ejercicio (3) me parece que te estás confundiendo nuevamente lo que el ejercicio llama el espacio vectorial V, con lo que puede ser un subespacio S del espacio vectorial V (tomando de ejemplo lo hablado en el ejercicio 1.c, el espacio V podría ser $$\mathcal{M}_{3x3}$$ (de dimensión 9) y un subespacio S de dicho espacio vectorial sería las matrices simétricas de 3x3 (de dimensión 6)). En este caso, tanto $$\mathbb{R}^4$$ como $$\mathbb{R}_{3}[x]$$ tienen dimensión 4, por lo que tu base tendrá 4 vectores, es decir que tendrás que agregar 2 vectores a cada uno de los conjuntos dados para completar la base.

En el ejercicio (4), para hallar las coordenadas tenés que usar los vectores originales, no utilizar la matriz una vez escalerizada, ya que estarías cambiando los vectores también. En la parte (a) entiendo que lo hiciste correctamente, pero me parece que en la parte (b) cambiaste estos vectores (por ejemplo, en la matriz que multiplica a w aparece un 11/3 que originalmente no estaba en la base, esas matrices deben ser las mismas que aparecen originalmente en la base). 

Para el ejercicio (5) primero que nada te recomiendo utilizar otros parámetros, ya que estás usando dos veces el $$\alpha$$ cuando en realidad son distintos. Lo ideal para este tipo de ejercicios es colgar los vectores $$p_1,p_2,p_3$$ para formar la matriz, y luego escalerizarla. Considerando que un polinomio de grado 2 se puede escribir como un vector de $$\mathbb{R}^3$$, expresando solamente los coeficientes (esto implica que, por ejemplo, al vector $$1+t$$ le corresponda el vector (1,1,0)), la matriz con los vectores colgados quedaría $$\left(\begin{smallmatrix}1&1&1\\1& \alpha &0\\0&1&1\end{smallmatrix}\right)$$. Escalerizando esta matriz y analizando los distintos valores de $$\alpha$$ se resuelve el ejercicio.

Por último, en el ejercicio (6) el procedimiento es correcto. El Ker(A) simplemente es el conjunto de vectores X que son solución al sistema AX=0. La forma de hallar su dimensión es, una vez que determinás Ker(A), simplemente hallar una base de dicho subespacio (similar a lo que hiciste en el ejercicio 1). En la parte (a), por ejemplo, dado que $$Ker(A)=\{a,-2a,a\}$$, podés determinar que una base de dicho subespacio sería $$[(1,-2,1)]$$, por lo que su dimensión es 1. De la misma manera, en la parte (b), justamente como Ker(A) te quedó en función de dos parámetros (c y d), si hallás una base de ese subespacio, vas a llegar a que tiene 2 vectores, por lo que la dimensión de Ker(A) es 2, cumpliendo la igualdad de dim(Ker(A))+rg(A)=n.

El ejercicio 2 está correcto.

Cualquier cosa que se me haya pasado o no haya quedado bien explicada no dudes en volver a preguntar.

Saludos
En respuesta a Martin Eduardo Kenny Pujadas

Re: Algunos ejercicios de la parte 1

de Nataly Melanie Ruber Maimo -
Hola, gracias!! pude entender bastante, sin embargo me quedaron un par de dudas,


en el caso del ejercicio 3b, capto por qué es de dimensión 4, y ya entendí por qué tengo que buscar otros dos vectores, sin embargo, tengo el tema de que al plantear la matriz me queda muy rara, como te pasé en la foto, me queda a-b y b-a que son dependientes, pero no sé si es que lo tengo mal planteado, aunque creo recordar que era la forma común de hacerlo con polinomios, agrupar los términos con grado semejante y así


Luego, escalericé la 1,5 y me dio que alfa no puede ser ni 1 ni 0, porque sino no es libre, ya que para que sea LI no puede ser determinado, es así, verdad?


Listo, esas son mis únicas dudas, gracias!!!!!

En respuesta a Nataly Melanie Ruber Maimo

Re: Algunos ejercicios de la parte 1

de Martin Eduardo Kenny Pujadas -

El ejercicio 3 no tiene una única forma de realizarse, existen infinitos vectores que completen S hasta obtener una base. Una manera de verlo a partir de lo que planteaste en la imagen que subiste es que dado que con el conjunto S original siempre vas a poder hallar valores de $$\alpha$$ y $$\beta$$ para generar $$a_0$$ y $$a_1$$, te faltaría solamente dos vectores (como ya dijimos antes, por la dimensión del espacio vectorial) para "completar" el polinomio, generando $$a_2$$ y $$a_3$$. Dado que esos coeficientes son los que multiplican a $$x^2$$ y $$x^3$$ respectivamente, agregando esos dos vectores llegás a que $$S=\{1-x+x^2,x-x^2,x^2,x^3\}$$ es una base de $$\mathbb{R}_3[x]$$ (lo podés comprobar vos misma). 

En el ejercicio 5 debería quedarte que la matriz queda de rango 3 para $$\alpha\neq0$$. Por lo que solamente si $$\alpha=0$$ el conjunto $$\mathcal{A}$$ no sería una base de $$\mathbb{R}_2[t]$$. Además recordá que para que sea LI el sistema homogéneo debe ser compatible determinado.

Saludos
En respuesta a Martin Eduardo Kenny Pujadas

Re: Algunos ejercicios de la parte 1

de Nataly Melanie Ruber Maimo -

Hola, había tenido mal la matriz, graciass


Probé lo que me dijiste y pareciera que sí funcionó


Lo único que no termino de comprender, es por qué falta generar a2 y a3, puesto que a simple vista yo no relacionaría 1-x+x² y x-x² con a0 y a1, sino que pareciera que hay mezcla de todas menos a3, por ejemplo cuando junto las cosas y digo x²(alfa-beta) yo interpreto que ambos alfa y beta son de a2, y cuando digo x(beta-alfa) pienso que ambos son de a1, y así con el resto, pero no hay ningún x³, por eso pensé en que era lo que faltaba, lo único que se me ocurre es que puesto que hay allí una dependencia, que sí sea lo que yo había pensado desde un principio de que hay que borrar los de a2 por ser dependiente de a1?


Gracias por la ayuda!!, perdona las molestiass

En respuesta a Nataly Melanie Ruber Maimo

Re: Algunos ejercicios de la parte 1

de Martin Eduardo Kenny Pujadas -

Como decís, no resulta difícil darse cuenta que el vector $$x^3$$ es uno de los que falta. Por otro lado, es verdad que el otro vector no resulta tan evidente.

La interpretación del resultado al cual llegaste en la primer foto que subiste, donde tenías $$a_3=?$$ y $$a_2=?$$ es que con esos dos vectores no podés generar todo el espacio $$\mathbb{R}_3[x]$$, ya que si pudieras generar dicho espacio, esos dos coeficientes te quedarían igualados a alguna combinación lineal de los multiplicadores que consideraste antes (en tu caso $$\alpha$$ y $$\beta$$). Si hubieses planteado $$x^2(\alpha-\beta)$$ entonces te habría quedado $$a_1=?$$, y agregando el vector $$x$$ en lugar del vector $$x^2$$ también hubieses completado una base de  $$\mathbb{R}_3[x]$$ (eso lo podés verificar).

Otra manera de verlo que quizás te ayude a comprenderlo es que para que el sistema $$\alpha(x^2-x+1)+\beta(x-x^2)=a_3x^3+a_2x^2+a_1x^1+a_0$$ sea compatible determinado se debe verificar que $$a_3=0$$ y $$a_2=-a_1$$ (es decir, el espacio vectorial generado por $$\{x^2-x+1,x-x^2\}$$ es $$\{a_3x^3+a_2x^2+a_1x^1+a_0\in\mathbb{R}_3[x]:a_3=0,a_2=-a_1\}$$). Como vos lo que querés generar es todo el espacio vectorial $$\mathbb{R}_3[x]$$ (esto sería que el sistema planteado sea compatible determinado para cualquier valor que tomen $$a_3,a_2,a_1$$ y $$a_0$$), no un subespacio de éste, tenés que agregar vectores que no verifiquen las condiciones de $$a_3=0,a_2=-a_1$$. Agregando dos vectores que no cumplan esas condiciones vas a obtener una base.

Saludos