¿Se puede decir que una función es diferenciable en un punto sii se puede aproximar por un plano tangente de la forma 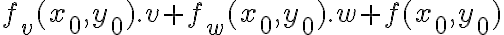 para todo
para todo 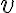 y
y 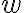 vectores L.I.?
vectores L.I.?
Entonces por ejemplo, la función:
no sería diferenciable en (0,0), ¿verdad?
Hola Juan, estoy de acuerdo con la propiedad que enuncias pero hay que dejar claro a qué nos referimos con "se puede aproximar por un plano tangente".
Esa precisión es exactamente la definición de diferenciabilidad. Esta dice que 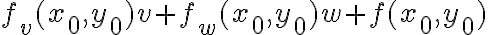 y
y 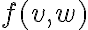 difieren en un resto cuyo orden de infinitésimos en
difieren en un resto cuyo orden de infinitésimos en 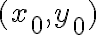 es mayor al de
es mayor al de 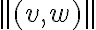 .
.
Estoy de acuerdo también con que la función que planteás no es diferenciable en  y está buena la intuición que manejás al notar que no hay un plano tangente. También fijate que si quisieras demostrar la no diferenciabilidad de un modo sencillo y concreto, podés probar que no existe alguna derivada direccional (por ejemplo
y está buena la intuición que manejás al notar que no hay un plano tangente. También fijate que si quisieras demostrar la no diferenciabilidad de un modo sencillo y concreto, podés probar que no existe alguna derivada direccional (por ejemplo 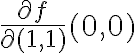 ).
).