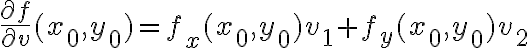Foro de Teórico

Hola Juan. Es así como lo planteás. Si tenés un vector dirección 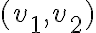$(v_1, v_2)$ (creo que no aportó mucho escribirlo en coordenadas polares), la derivada direccional respecto a él puede escribirse como combinación lineal de las derivadas parciales, es decir

$\frac{\partial f}{\partial v} (x_0, y_0) = f_x(x_0, y_0) v_1 + f_y(x_0, y_0) v_2$.

Esto se debe a que el vector gradiente en 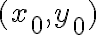$(x_0, y_0)$ es la matriz asociada a una transformación lineal (el diferencial), que lo que hace es, dado un vector 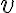$v$, devuelve $\frac{\partial f}{\partial v} (x_0, y_0)$.

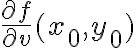Esto tiene sentido solo cuando esa transformación existe, es decir cuando la función es diferenciable. Es importante verificar eso (y no la sola existencia de las derivadas parciales) para poder utilizar esa propiedad.

Como ejemplo de función (no diferenciable) cuyas derivadas direccionales parciales existen pero no cumplen esa igualdad sugiero ver el ejercicio 13 del práctico 8.