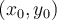Buenas, mi duda es la siguiente:
Para saber si una función es diferenciable en un pto (xo,yo) lo primero es estudiar la continuidad en ese punto. Si es continua, procedo a calcular las derivadas parciales, para lo cual, como se menciona, hay dos formas; o bien aplicar directamente la definición y calcular el lim del cociente incremental, o derivar la función, por lo general en puntos genéricos "lejanos" al problemático (xo,yo) y hacer el lim cuando x,y tienden a (xo,yo), siempre y cuando las derivadas parciales sean continuas en (xo,yo). Con este limite calculado tendria el valor de las derivadas parciales en (xo,yo). La primer pregunta que tengo es que si yo calculo las derivadas parciales por el primer metodo ¿no deberia tambien chequear que estas son continuas en (xo,yo)? La segunda es si, afirmando ya sea en el segundo caso o en el primero (de ser afirmativa la respuesta a mi primer pregunta) que las derivadas son continuas en el punto, por el teorema de la condicion suficiente de diferenciabilidad, podria asumir la diferenciabilidad en ese punto, o ademas tengo que ver que las derivadas parciales existen en una bola de centro (xo,yo). Otra duda que me surge en este momento es que como la bola puede ser de un tamaño relativamente grande, si las derivadas parciales deberian existir en todo punto de la funcion para que sea diferenciable en el pto (xo,yo).
Por ultimo, me pregunto en que momento me veria obligado a ver si el limite del resto evaluado en el incremento sobre la norma de este incremento tiende a cero para ver si la funcion es diferenciable.
Saludos