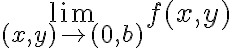Ok, creo que ahora entendí mejor.
La respuesta es que la idea tiene cosas bien pero no es exactamente así. Recordemos que una función es contínua si es contínua en cada uno de sus puntos. Entonces para estudiar la continuidad de la función, estudiamos la continuidad en 
, para todo punto del dominio.
Entonces en un ejercicio como el 11c) para estudiar continuidad en podemos considerar tres situaciones:
- Cuando está en la región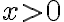
, es decir, cuando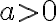 
- Cuando está en la región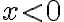
, o sea,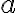 
- Cuando está en la región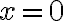
, es decir, cuando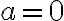 
En los dos primeros casos la función es contínua porque es punto interior de la región donde la función está definida de una u otra forma. Así, en el caso 1 por ejemplo la función es contínua porque la expresión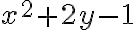 
lo es.
es punto interior de la región donde la función está definida de una u otra forma. Así, en el caso 1 por ejemplo la función es contínua porque la expresión 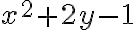lo es.Lo más delicado es el tercer caso, que es donde viene tu pregunta. Si estamos estudiando la continuidad en un punto de dicha región, sabemos que 
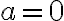por lo que el punto es 
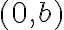, donde 
es arbitrario pero fijo. Por lo tanto, el límite que querés estudiar es
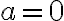de dicha región, sabemos que por lo que el punto es 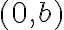, donde es arbitrario pero fijo. Por lo tanto, el límite que querés estudiar es
Fijate que no hablé de tender por izquierda ni por derecha, ya que podría acercarme al punto en cuestión por cualquier curva. Lo que sí sabemos es que si me acerco por una curva totalmente incluida en la región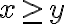 
, entonces el límite será 
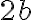(porque uso la primer expresión) Y si me acerco por una curva incluída en la región 
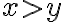el límite será 
.
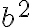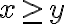, entonces el límite será 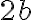(porque uso la primer expresión) Y si me acerco por una curva incluída en la región 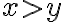el límite será 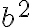.Eso nos da una herramienta para negar continuidad en ciertos puntos. Si es de tal modo que 
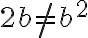, la función no será continua en 
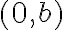¿Y si caso 
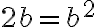? Se puede probar que en esos puntos la función sí es contínua. Es un ejercicio interesante, y básicamente consiste en usar la definición de continuidad para, a partir del hecho de que en cada una de los interiores de las regiones es contínua, encontrar un entorno adecuado para verificar la definición de continuidad en los 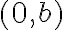adecuados.
es de tal modo que 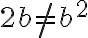, la función no será continua en 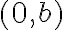¿Y si caso 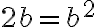? Se puede probar que en esos puntos la función sí es contínua. Es un ejercicio interesante, y básicamente consiste en usar la definición de continuidad para, a partir del hecho de que en cada una de los interiores de las regiones es contínua, encontrar un entorno adecuado para verificar la definición de continuidad en los 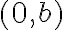adecuados.En resumen, sospecho que el resultado del ejercicio va a ser similar al que estabas pensando, pero los fundamentos tenían algunos problemas. Espero que ahora se haya ordenado un poco más. Saludos