La diferencia es que en la parte a) estás manipulando simultaneamente ambas variables. Por eso terminás probando una condición necesaria y suficiente para que el límite sea  . Porque al cuantificar
. Porque al cuantificar 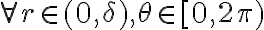 estás tomando una bola de centro en el origen y radio
estás tomando una bola de centro en el origen y radio 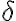
En la parte b en cambio, lo que haces es para cada  fijo tomar límite con
fijo tomar límite con  tendiendo a cero. Esto es lo mismo que acercarse al origen sólo por (semir)rectas. Si el límite de la función es
tendiendo a cero. Esto es lo mismo que acercarse al origen sólo por (semir)rectas. Si el límite de la función es  , también lo será al acercarse por cada una de las semirrectas. Sin embargo el recíproco no vale y por eso en b) se prueba una implicancia sola. Esta última idea se desarrolla después y hay que probarla en la parte d).
, también lo será al acercarse por cada una de las semirrectas. Sin embargo el recíproco no vale y por eso en b) se prueba una implicancia sola. Esta última idea se desarrolla después y hay que probarla en la parte d).
Saludos
