Está buena la pregunta y es bastante sutil, pero esa definición alternativa de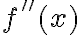 
sirve siempre y cuando existan las derivadas. Si bien en la cuenta no se usa la derivada primera, se demuestra usando Taylor y se requiere para ello la existencia de dicha derivada.
Podría decirse entonces que la derivada segunda es cero, en los puntos en que la derivada existe (es decir en todos los reales excepto el cero). Esto tiene sentido ya que en dichos valores la función es lineal.