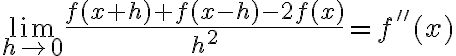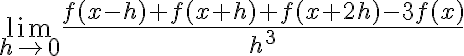Noción de derivadas

Noción de derivadas

de Juan Agustín Rivero Szwaicer -
Número de respuestas: 4
Esta pregunta no tiene que ver mucho con los temas del curso, nomás es una duda que me surgió y no sé dónde evacuarla porque cada clase tiene su rutina planificada y no me gusta interrumpir la continuidad de las clases con temas que no tengan que ver con lo que se está dando.

El razonamiento es el siguiente: así como la derivada primera es la pendiente de una gráfica (en una variable), y se puede medir a partir de dos puntos en la gráfica que tienden a pegarse entre sí; como la derivada segunda es la amplitud de arco de parábola, ¿se puede medir a partir de 3 puntos de alguna forma?

La idea de esto es darse cuenta un poco de forma más intuitiva de los valores de derivada de diferentes órdenes de una gráfica en un cierto punto.

Saludos
En respuesta a Juan Agustín Rivero Szwaicer

Re: Noción de derivadas

de Alejandro Bellati -

Hola, interesante pregunta

Primero déjame decir que la derivada primera es límite de la pendiente de una gráfica de una variable, y uno intuye su valor mirando con dos puntos que tienden a pegarse tal cual decís.


Bueno, efectivamente la derivada segunda se puede medir a partir de tres puntos. Se puede probar que

\lim_{h\to 0}\frac{f(x+h)+f(x-h)-2f(x)}{h^2} = f''(x)


No se qué tan intuitivo puede ser mirar 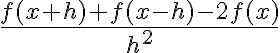\frac{f(x+h)+f(x-h)-2f(x)}{h^2} a ojo de una gráfica, pero al menos es una respuesta.

Para demostrar la fórmula que puse podes usar taylor. 

Saludos!
En respuesta a Alejandro Bellati

Re: Noción de derivadas

de Juan Agustín Rivero Szwaicer -

Wow, no conocía ese límite. Supongo que debe haber forma de calcular derivadas de diferente orden de esa forma así sistemática. Algo como \lim_{h\rightarrow 0}\frac{f(x-h)+f(x+h)+f(x+2h)-3f(x)}{h^{3}} para orden 3. Capaz que la parte intuitiva es que lo que valga en f(x) influye cada vez más en la derivada, se me ocurre... Gracias!!
En respuesta a Alejandro Bellati

Re: Noción de derivadas

de Juan Agustín Rivero Szwaicer -

Nomás por curiosidad. Según esa definición, se puede decir que la segunda derivada del valor absoluto de x es siempre cero? Porque donde tiene problema en la primera derivada, en el cero, se resuelve con esta definición y quedaría lim (h-h-2*0)/h² y eso da cero, está bien?

En respuesta a Juan Agustín Rivero Szwaicer

Re: Noción de derivadas

de Veronica Rumbo -

Está buena la pregunta y es bastante sutil, pero esa definición alternativa de 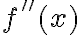f''(x) sirve siempre y cuando existan las derivadas.  Si bien en la cuenta no se usa la derivada primera, se demuestra usando Taylor y se requiere para ello la existencia de dicha derivada.

Podría decirse entonces que la derivada segunda es cero, en los puntos en que la derivada existe (es decir en todos los reales excepto el cero). Esto tiene sentido ya que en dichos valores la función es lineal.