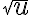Buenas tardes.
La pregunta tiene un enfoque en el ejercicio, pero sobre todo en ¿Cuando puedo hacer un cambio de variable valido en un limite?
Por ejemplo: en este ejerció tenemos que ver si este limite converge.
que también seria lo mismo que decir ![\lim_{(x.u)\to (0,0)} \frac{\sqrt[]{u}}{2} . \frac{2x.u}{x^2 + u^2} \lim_{(x.u)\to (0,0)} \frac{\sqrt[]{u}}{2} . \frac{2x.u}{x^2 + u^2}](https://eva.fing.edu.uy/filter/tex/pix.php/90a2222de52c630788a882d33dcaa1fc.gif)
Ahí podemos ver fácilmente que 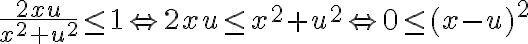 lo cual siempre se cumple.
lo cual siempre se cumple.
Quedando algo que tiene a 0, por una acotada, lo cual es 0 por la parte anterior.
Mi pregunta sobre todo es, ¿Cuando estoy habilitado a hacer un cambio de variable en una sola de las variables variables?
Saludos
Daniel

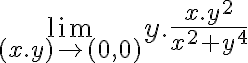
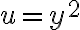
![\lim_{(x.u)\to (0,0)} \sqrt[]{u} . \frac{x.u}{x^2 + u^2} \lim_{(x.u)\to (0,0)} \sqrt[]{u} . \frac{x.u}{x^2 + u^2}](https://eva.fing.edu.uy/filter/tex/pix.php/857b0344778165aa41595ea0470d8efa.gif)