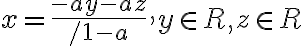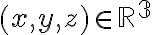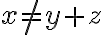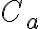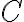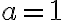Buenas, en el ejercicio 2 del práctico, piden que hallemos el dominio y conjuntos de nivel, no se bien a que se refiere.
Interprete que con escribir una variable en función de la otra, ya estaba.
Por ejemplo en el 2.a, me quedó que el dominio es:
D={(x,y,z): x
y+z}
Mientras que los conjuntos de nivel, me quedaron:
C={(x,y,z): 
}
No se si es esto, en caso de que no, que es lo que debería hacer?
Gracias, saludos!
Lo que tenés que hacer para determinar el dominio es decir para qué puntos puede definirse la función. En el 2a) por ejemplo el dominio es exactamente ese que dijiste (que es donde no se anula el denominador).
Creo que tu duda viene de si esa es la manera de representarlo, y mi respuesta es sí: Fijate que lo que vos escribiste puede leerse como "El conjunto de los puntos 
(está bueno decir dónde están los puntos) tales que 
".
El conjunto de nivel también está (casi casi casi) bien. Para mejorar un poquito la escritura, lo llamaría 
en vez de 
, cosa de que se entienda que es el conjunto de nivel asociado a un 
fijo (y que si cambia también lo hará el conjunto). En particular, faltaría indicar qué sucede en el caso 
, en el cual el conjunto no puede definirse del modo que lo hiciste.
Saludos.