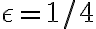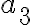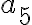Buenas.
Tengo una duda en una parte especifica de la demostración.
Cuando estamos trabajado con un rango de infinitos elementos, por medio del anterior teorema (Bolzano - Weierstrass) me garantiza que hay un punto de acumulación. Por lo tanto vamos construyendo punto a punto la sub-sucesion tomando los radios cada vez mas chicos.
Mi pregunta es, como uno puede estar seguro que el indice del 'an' sea mayor a todos los anteriormente seleccionados.
En otras palabras. Si para epison < 1/2 elegí a a5. Como puedo saber que cuando epison sea < 1/4 el an que voy a elegir tiene un indice necesariamente sea mayor. Pense que podría ser porque hay infinitos puntos, pero no se si esto sea prueba suficiente.
¿Me pueden ayudar con esto?
Saludos
Daniel