Foro de Ejercicios fuera de los Prácticos

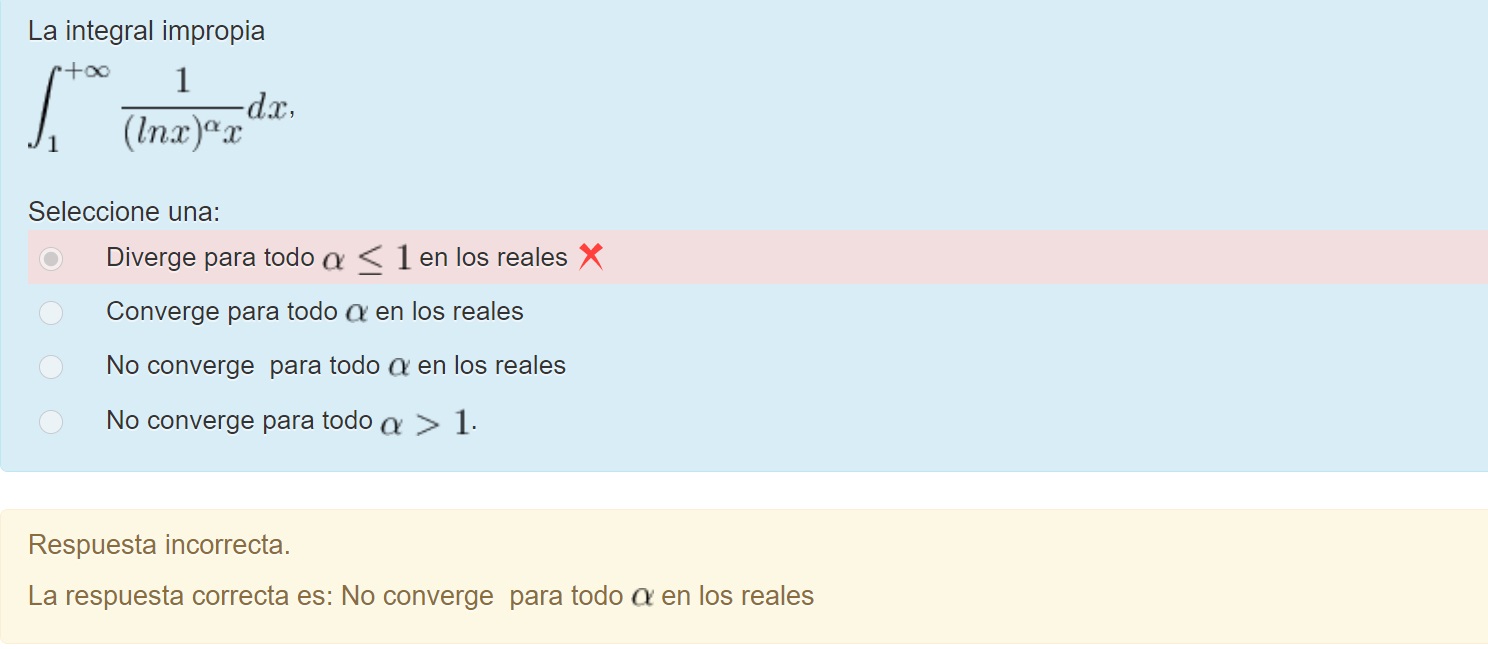
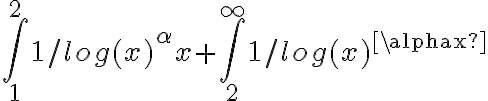Buenas, para hacer el ejercicio adjunto, separe en dos la integral:

$\int_{1}^{2}{1/log(x)^ \alpha x} + \int_{2}^{ \infty }{1/log(x)^ \alphax}$, la integral me quedó:

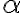(log(x)^(-$\alpha$+1)) /$\alpha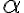$+1), evaluado en cada parte a lo que corresponde.

Por lo que, en la primer integral converge si ( \alpha \)<1, y diverge si ( \alpha \)>1.

Mientras que en la segunda, me quedó que:

Converge si ( \alpha \)>1

Diverge si ( \alpha \)<1.

Y el caso igual 1 me quedó que diverge.

Por lo que, tendría que diverge para todos los alfas.

La solución dice que, "no converge para todos los alfas", o sea que hay al menos uno para el que converge, no?

No entiendo donde le erre.

Tampoco entiendo cuando puedo decir si diverge o no, porque por lo que tenía entendido, divergía si el limite era mas o menos infinito, y así es como queda en estos casos, pero no dicen que diverge, sino que no converge.

Gracias, saludos!