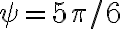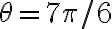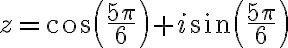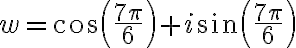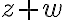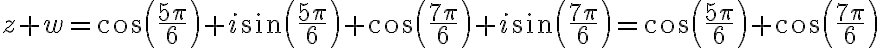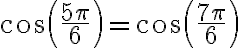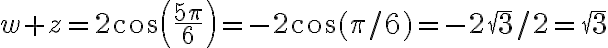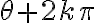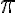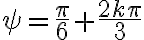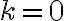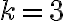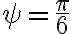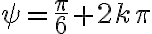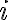Buenas, tengo dudas respecto al método que se debe seguir para resolver este ejercicio, si bien ya intente resolverlo de varias maneras, no logro ver cual es el razonamiento que se debe seguir para llegar al resultado correcto.
Desde ya, muchas gracias.
Francisco.
(Adjunto imagen del ejercicio con la respuesta correcta marcada)



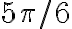
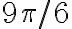
![[\pi/2, \pi] [\pi/2, \pi]](https://eva.fing.edu.uy/filter/tex/pix.php/003480bdd73b4a9469bfe8ea4b0fce4a.gif)