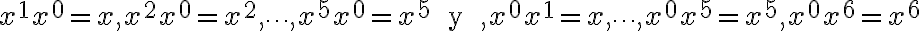Buenas, no entiendo la resolución del primer ejercicio de desarrollo. "Tirar un dado es equivalente a elegir uno de los términos (x+x 2+x 3+x 2+x 5+x 6 ), pero como al salir 6 tiramos de nuevo, sería equivalente a (x+x^2+x^3+x^4+x^5+x+x^2+x^3+x^4+x^5+x^6 )", no entiendo por qué sumar todos los términos dos veces menos el de x^6 sería equivalente a que cuando saco 6 tiro de nuevo, cómo seria ese razonamiento. Por otro lado tampoco sigo el procedimiento que hace la solución para hallar el coeficiente de x^6.
A ver si pensarlo de esta forma ayuda:
Cada tirada es la suma de dos números: i+j
Si sacas del 1 al 5 en el dado, i= el valor que sacaste y j=0 (no volves a tirar)
Si sacas 6, i=0 y j=valor que sacas al tirar de nuevo
Entonces las posibles exponentes vienen de los posibles 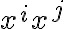
Las posibles tiradas son entonces
Buenas tardes. Para mi también resulta un poco confusa esa frase, yo lo entendí mejor así:
Veamos cual es la función generatriz f(x) que cuenta las formas de obtener n con 1 tirada validada:
Hay dos formas de obtener 1: 1 ó 61 (obtener 1 de primera, u obtener un 6 que resulta invalidada y luego un 1); entonces el coeficiente de x es 2.
Hay dos formas de obtener 2: 2 ó 62; entonces el coeficiente de x^2 es 2.
...
Hay dos formas de obtener 5: 5 ó 65; entonces el coeficiente de x^5 es 2.
Hay una forma de obtener 6: 66 (la única forma de obtener un 6 validado es haber sacado antes un 6 invalidado); entonces el coeficiente de x^6 es 1.
Por lo tanto, f(x)= 2x+2x^2+2x^3+2x^4+2x^5+x^6.
Para 5 tiradas validadas entonces la función generatriz f(x) que cuenta las formas de obtener n con 5 tirada validadas será igual a (2x+2x^2+2x^3+2x^4+2x^5+x^6)^5. Nos interesa aquellas tiradas que nos hacen obtener 11 por eso la respuesta es el coeficiente de x^11 de ese producto.
Igual no te preocupes mucho, me pareció un ejercicio interesante pero un poco difícil talvez para un parcial. Este parcial estará más acorde a los ejercicios del práctico.
PD. Acabo de ver la respuesta de Mariana y también está buena esa forma de pensarlo.
Las dos maneras son muy claras, graciaas.