Foro de Ejercicios fuera de los Prácticos

Hola Diego, para entender el segundo ítem es clave tener en cuenta cómo funciona el producto de complejos. En particular que al multiplicar dos complejos sus módulos se multiplican y sus ángulos se suman. Por lo que elevar al cubo tiene el efecto de multiplicar el ángulo por 3.

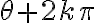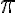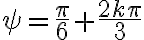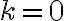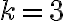Por otro lado, es lo mismo tomar un ángulo $\theta$ que $\theta + 2k\pi$ para cualquier $k$ entero, ya que el ángulo $\pi$ corresponde a dar toda la vuelta al círculo. Es decir que los ángulos que buscamos son los de la forma $\psi = \frac{\pi}{6} + \frac{2k\pi}{3}$ con k entero. Sin embargo, se "repiten" valores, en el sentido de que para $k = 0$ y $k = 3$ por ejemplo, obtenemos el mismo complejo: para 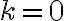$k = 0$ tenemos 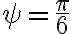$\psi = \frac{\pi}{6}$ y para 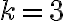$k = 3$ se tiene 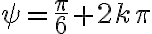$\psi = \frac{\pi}{6} + 2k\pi$ (que es el mismo ángulo). En total hay solo tres valores de 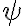$\psi$ que correspondan a puntos distintos.

Te sugiero que representes en el plano los distintos $z$ posibles según las cuentas y ahí creo que va a quedar claro eso de que son sólo tres puntos posibles (las tres raíces cúbicas de $i$).

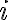Saludos.