Hola María. Efectivamente es un si y sólo si. 
es cerrado si y solo si 
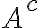es abierto.
Al respecto, una cosa que me gusta pensar es que dado un conjunto cualquiera (llamémosle 
), el espacio en el que está dicho conjunto queda particionado en tres subconjuntos, a saber
- El de los puntos que están "bien dentro" de , también conocido como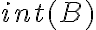
(interior de ). - El de los puntos "del bordecito", es decir, la frontera de que notamos como
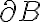. (nótese que estos puntos pueden o no estar en ) - El de los puntos exteriores a . Estos son, los puntos interiores a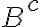
. Este conjunto se nota como 
.
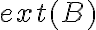¿Por qué hago esta observación? porque es útil para pensar la topología de . Fijate que el interior siempre está incluido en y el exterior siempre tiene intersección vacía con . Lo que puede variar según el caso es el comportamiento de la frontera.
. Fijate que el interior siempre está incluido en y el exterior siempre tiene intersección vacía con . Lo que puede variar según el caso es el comportamiento de la frontera.Entonces si 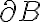está incluido en tenemos que es cerrado. Y si es disjunta con (es decir,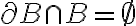 
) el conjunto es abierto. Cualquier otra cosa que pase con la frontera, denota conjuntos que no son abiertos ni cerrados.
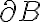está incluido en tenemos que es cerrado. Y si es disjunta con (es decir, 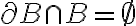) el conjunto es abierto. Cualquier otra cosa que pase con la frontera, denota conjuntos que no son abiertos ni cerrados.Esta manera de pensarlo creo que ayuda a entender el por qué de ese si y solo si.
Saludos.