Buenas,
En este ejercicio se sugiere una forma para el potencial con dos constantes a determinar. Se me ocurre aplicando condiciones de borde la condición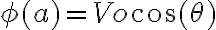 
, de dónde tengo 
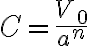. Sin embargo, no se me ocurre que otra condición aplicar para determinar n.
Desde ya gracias.
La otra condición a aplicar es que el potencial verifique la ecuación de Laplace. Esto es porque el sistema está en régimen estacionario, entonces de la ecuación de continuidad 
. Como el material es óhmico también tiene que valer 
, y de ahí 
.
Buenas Ricardo, hice lo que propusiste y llegue a que mi n puede tomar 2 valores, plantie el laplaciano del potencial y llegue a que para que valga cero n tiene que cumplir la ecuacion: n^2+n-2=0, de donde salen los valores 1 y -2.
¿Como diferencio con que valor me tengo que quedar?
Facundo, todo bien?
El ejercicio te pide que encuentres el potencial dentro de la esfera, lo cual quiere decir que tu potencial tiene que valer también para r=0, esto te permite descartar el término con n<0, ya que si estuviera, el potencial divergería en el origen. Por eso te quedas con el n=1.
Espero que haya quedado claro, cualquier cosa pregunta de nuevo.
Suerte!