ejercicio 1

ejercicio 1

de Ignacio Miranda Guerrero -
Número de respuestas: 4
Hola,porque el campo eléctrico de un capacitor de placas rectangulares no es sigma/epsilon0 y es sigma/2epsilon0. porque en realidad en teórico vimos que sobre la superficie de cualquier conductor el campo eléctrico muy cerca es la primera expresión. lo que no entiendo es que se puede tomar perfectamente el cilindro desde el conductor y por eso da la primera que me parece razonable y la segunda para mi corresponde a el de la placa cargada. sin embargo si tomo la segunda expresión ta hallo la fuerza integrando y queda la solución de la respuesta. pero no entiendo porque, parece que fuera lo mismo si es conductor  o no es conductor y parece que fuera lo mismo tomarse el cilindro con la tapa en la placa o el cilindro a los costados de la placa.
En respuesta a Ignacio Miranda Guerrero

Re: ejercicio 1

de Guzman Hernandez -

Hola,

El campo eléctrico dentro del condensador es efectivamente 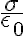 \frac{\sigma}{\epsilon_0} . Lo que sucede es que para hallar la fuerza sobre una de las placas, hay que considerar solamente el campo generado por la otra. Y el campo generado por una sola de las placas es  \frac{\sigma}{2\epsilon_0} . 

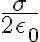Espero que esto te aclare las cosas.

Cualquier cosa no dudes en repreguntar

saludos

G
En respuesta a Guzman Hernandez

Re: ejercicio 1

de Ignacio Miranda Guerrero -

eso yo lo entiendo, lo que digo es que en el teórico hay una clase que habla de que en cualquier conductor. el campo muy cerca del conductor vale σ/ϵ0 porque se toma el cilindro en la superficie del conductor y para afuera, tipo una de las tapas toca la superficie del conductor entonces ta ahí el campo vale 0. yo entiendo el  resultado. pero porque ese resultado teórico no es valido si el campo adentro del condensador es producido una placa conductora. 

En respuesta a Ignacio Miranda Guerrero

Re: ejercicio 1

de Ricardo Marotti -


Ese resultado sigue siendo válido para el campo total generado en la superficie de la placa del condensador. Pero para hallar la fuerza que se realiza sobre una placa no se considera el campo total, si no solo la parte del campo que genera la otra placa. Hay que restarle al campo total el campo propio. Eso es lo mismo que te respondió Guzmán. Tené en cuenta que el campo vale σ/ε0 del lado de afuera de la placa, y cero dentro. O sea que hay una indeterminación de cuanto vale el campo total exactamente en la superficie. 

Para ver esto en detalle te recomiendo que mires desde el minuto 42:40 al minuto 55 de la clase 3 de OpenFing. Allí se discute cuál es el campo total en la superficie de un conductor, y cuál es el campo propio, que hay que restarle al campo total, para hallar el campo que actúa sobre cada elemento de carga de la superficie de un conductor. También se calcula la fuerza que se realiza sobre una placa de un condensador.