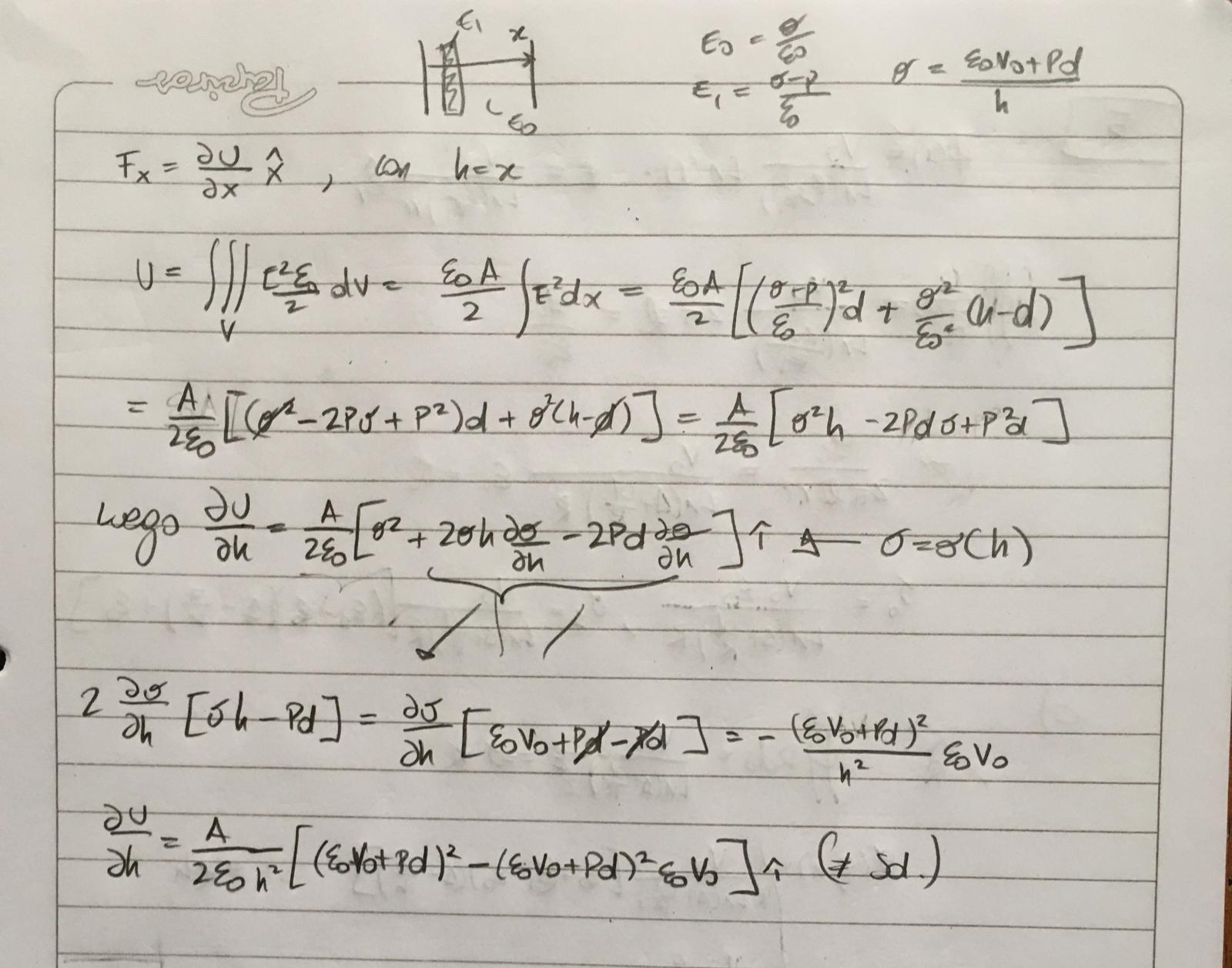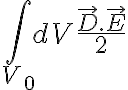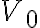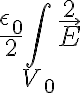Hola, me da distinto a la solución en este ejercicio y creo que es por tomar que la densidad de carga es una función de h, entonces al derivar la energía en función de h me aparecen términos adicionales a la solución. Quería saber si eso estaba mal, o quizás tengo algún otro error que no encontré. Adjunto el desarrollo.
Muchas gracias
La letra del ejercicio dice: "Suponga ahora que se desconecta la batería V0, y el sistema (placas + material con polarización permanente) permanece aislado.". Esto significa que las cargas en las placas son constantes, y también lo será la densidad de carga. Vos, al derivar la densidad de carga, estás considerando que el potencial es constante, y según esa frase no lo es, porque la batería está desconectada.
Otra observación de tu solución es que no tenemos una expresión de la energía para un material con polarización permanente. Pero sin embargo, como los campos en ese material, ni su forma, dependen de h (a densidad de carga constante en las placas), la energía almacenada en él será constante y solo variará la energía almacenada en el vacío entre las placas.
Aaa bien entiendo, me olvidé de eso. Entonces para calcular la energía en el vacío U, ¿puedo hacerlo integrando DE/2 en el volúmen?
Si, la energía en el vacío puede calcularse como 
donde 
es el volumen ocupado por el vacío. O lo que es lo mismo: 
.