Hola Manuel,
Para separar la integral como suma de dos integrales es necesario saber que ambas convergen (a veces se puede seguir desarrollando las cuentas y confirmarlo a posteriori, pero debemos confirmar que esto suceda). La razón de esto es la misma que por la que pasaba eso en los límites, de hecho esto sucede porque la integral es un límite. Por ejemplo si tenemos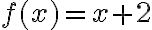 y
y 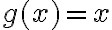 , al calcular
, al calcular 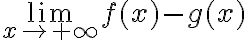 no podemos igualarlo a
no podemos igualarlo a 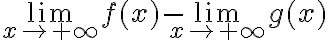 . En este caso en la penúltima igualdad lo que tenes es un sumando que es
. En este caso en la penúltima igualdad lo que tenes es un sumando que es 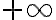 y dos sumandos que son
y dos sumandos que son 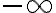 , lo que es una indeterminación, que según el
, lo que es una indeterminación, que según el  va a tener resultados distintos.
va a tener resultados distintos.
Un camino posible es tomar denominador común al principio, obtener la función como un único cociente de polinomios y estudiar cuándo converge. Otro camino posible, que usa el cálculo de primitivas que hiciste, es en lugar de evaluar las primitivas, unificar los dos sumandos de la primitiva de la función usando propiedades del logaritmo.
Saludos,
Leandro
Para separar la integral como suma de dos integrales es necesario saber que ambas convergen (a veces se puede seguir desarrollando las cuentas y confirmarlo a posteriori, pero debemos confirmar que esto suceda). La razón de esto es la misma que por la que pasaba eso en los límites, de hecho esto sucede porque la integral es un límite. Por ejemplo si tenemos
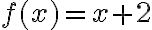 y
y 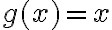 , al calcular
, al calcular 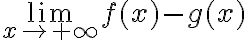 no podemos igualarlo a
no podemos igualarlo a 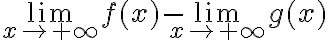 . En este caso en la penúltima igualdad lo que tenes es un sumando que es
. En este caso en la penúltima igualdad lo que tenes es un sumando que es 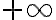 y dos sumandos que son
y dos sumandos que son 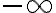 , lo que es una indeterminación, que según el
, lo que es una indeterminación, que según el  va a tener resultados distintos.
va a tener resultados distintos. Un camino posible es tomar denominador común al principio, obtener la función como un único cociente de polinomios y estudiar cuándo converge. Otro camino posible, que usa el cálculo de primitivas que hiciste, es en lugar de evaluar las primitivas, unificar los dos sumandos de la primitiva de la función usando propiedades del logaritmo.
Saludos,
Leandro
