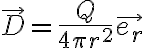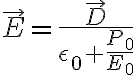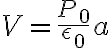En efecto, no conocés la capacitancia del sistema. Pero tampoco se precisa.
La idea es que tenés que separar el medio dieléctrico en dos regiones: una en la que el dieléctrico es lineal (la región exterior en que el campo es menor) y otra en que el dieléctrico satura (la región interior). Ojo que esto no implica que la polarización sea constante, porque la polarización es paralela al campo eléctrico, y el campo eléctrico tiene dirección radial, por la simetría esférica. La transición entre ambas regiones se da cuando tengo un radio que podemos llamar R y es lo que se pide en la parte bii. En R ambos campos eléctricos tienen que ser iguales a  .
.
Pero aplicando la ley de Gauss el desplazamiento eléctrico tiene la misma forma en ambas regiones:
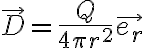
donde Q es la carga de la superficie conductora interior, r y  son los usuales de coordenadas esféricas. De allí obtenés el campo eléctrico en cada región en función de Q. Para la región lineal:
son los usuales de coordenadas esféricas. De allí obtenés el campo eléctrico en cada región en función de Q. Para la región lineal:
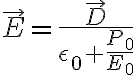
donde 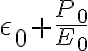 es la permitividad en la región lineal .
es la permitividad en la región lineal .
Para la región no lineal:

Igualando el módulo de estos campos a  en r = R se obtiene una primer relación entre Q y R.
en r = R se obtiene una primer relación entre Q y R. Luego integrando el módulo de los campos anteriores en r se obtienen las formas del potencial electrostático en las dos regiones. Al hacer esto aparecen dos constantes de integración, llamésmole A y B. Estas constantes se evalúan en función de Q haciendo que el potencial en r = 2a sea 0, y el potencial en r = a valga 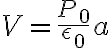
Finalmente hay que hacer que el potencial sea continuo en r = R (porque el campo eléctrico es finito). Esto da otra relación entre Q y R, que con la que se había obtenido antes se puede despejar R y Q. Y con eso se conocen las cantidades que piden las partes bi y bii.
De la polarización en cada zona se hallan las densidades de carga de polarización que se piden en biii.