Hola Rodrigo. En primer lugar la demostración no falla, la proposicion es cierta. Lo que se hace en el video es tomar como punto de partida un punto genérico de 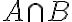 y probar que dicho punto es interior a
y probar que dicho punto es interior a 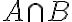 . Esto demuestra que el conjunto intersección es abierto ya que todo punto en él es interior.
. Esto demuestra que el conjunto intersección es abierto ya que todo punto en él es interior.
Esto vale también si los conjuntos son infinitos. Es importante notar que cuando en una demostración tomamos un elemento genérico y probamos que cumple algo (en este caso, un punto y probamos que es interior), lo que estamos haciendo es demostrar la propiedad para todo punto, ya que no asumimos ninguna hipótesis adicional sobre éste.
Ahora te devuelvo parte de tu pregunta. Vos decís que entendiste el caso en que la intersección es un solo punto. Yo pregunto ¿Puede pasar tal cosa? ¿Podrías dar un ejemplo de dos conjuntos abiertos cuya intersección sea tan solo un punto?
Saludos.
 y
y 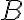 conjuntos abiertos
conjuntos abiertos 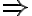
 es abierto.
es abierto.