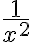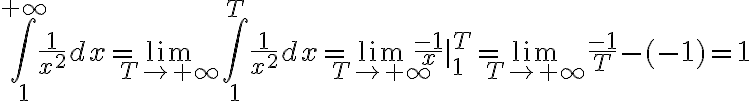Hola, en la clase 15 se plantea el ejercicio de resolver la integral impropia 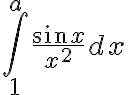
Lo que hice fue comparar la función tomando su valor absoluto, y observe que f(x)≤1/x^2.
Luego, sobre la impropia de 1/x^2 evaluada 1 a +∞, halle la primitiva -1/x e hice el limite de la función que es 0.
Mi duda es sobre la interpretación de este resultado. No logro entender como puede ser que el área bajo la curva sea 0, o si tengo algún error que no logro ver.