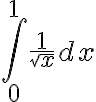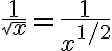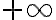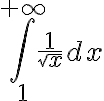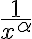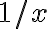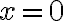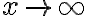Hola, en un momento de la clase, Fiori esta realizando un ejercicio de integrales impropias, donde hay que utilizar las integrales mixtas, luego de desarrollar la integral mixta, empieza analizar si esta convergen o no, pero en la primera por el criterio de de que si el exponente era mayor a 1 era convergente, y si era menor estricto, divergente, el caso es que a mi me parece que es divergente, pero como nadie de la misma clase pregunto no tengo ni idea, la parte que me refiero comienza en el minuto 20.
Gracias de antemano y saludos : )
Diego