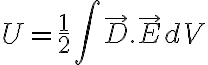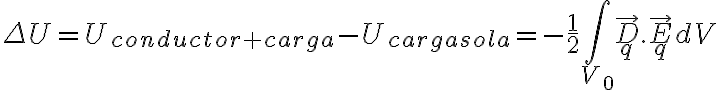Foro Práctico 3.

La energía electrostática para un medio lineal se puede calcular como: 

$U = \frac{1}{2} \int_{}^{}{ \vec{D} . \vec{E} dV}$

donde la integral debe evaluarse en todo el espacio. El integrando (con el factor 1/2 incluido) es lo que llamamos densidad de energía electrostática w. 

Ahora bien, aplicando ley de Gauss, los campos 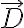$\vec{D}$ (desplazamiento eléctrico) y 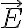$\vec{E}$ (campo eléctrico) son iguales en la región que no hay conductor (para el sistema descrito en el ejercicio y el de una carga colocada en el origen en el vacío). En el interior del conductor los campos valen cero (para el sistema conductor más carga). Así que la diferencia entre la densidad de energía electrostática para el conductor con la carga y la carga sola será cero en donde no hay conductor (se cancelan dos términos que son iguales). Pero en el interior del conductor son diferentes. La integral queda cero para el sistema conductor más carga en esa región y diferente de cero para la carga sola: 

$\Delta U = U_{conductor+carga} - U_{carga sola} = - \frac{1}{2} \int_{V_0}^{}{ \vec{D}_q . \vec{E}_q } dV$

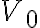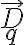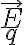donde $V_0$ es la región que ocupa el conductor y $\vec{D}_q$ y $\vec{E}_q$ son el desplazamiento eléctrico y el campo eléctrico de la carga sola ubicada en el vacío, respectivamente. Así que para responder la pregunta de este ejercicio hay que hacer esa integral.