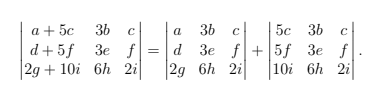Buenas, me encontraba haciendo este ejercicio y la única forma en la que llegué a su solución es esta, pero tengo la sensación de que está mal descompuesto, está bien?
Hola Claudio,
Siguiendo con la descomposición que planteas, la cual es correcta, sabés que la segunda matriz tendrá determinante nulo (ya que la primer columna es combinación lineal de la tercera), mientras que para hallar el determinante de la primer matriz conviene operar con los escalares que aparecen, determinando como modifican cada uno el valor del determinante (si te fijás la tercer fila está multiplicada por 2, mientras que la segunda columna está multiplicada por 3). Si no sale preguntá de nuevo.
Saludos
Buenas, Martin
No comprendo muy bien como calcular el discriminante a partir de la descomposición. Veo que se supone que un determinante de la desposición es nulo pero no entiendo bien por qué.
Será que me puedes guiar con eso.
Gracias de antemano.
Hola Gabriela,
La idea es aplicar la propiedad del determinante de aditividad (adjunto foto) y lograr que una de las matrices tenga determinante cero para facilitar los cálculos del determinante de la matriz original. En este caso la segunda matriz tiene determinante nulo ya que dos de sus columnas son proporcionales (la primera y la tercera verifican que $$C_1=5C_3$$).
Saludos