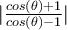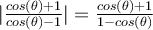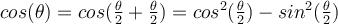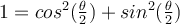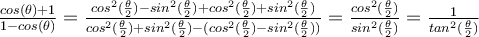Ejercicio 5, identidades trigonométricas

Ejercicio 5, identidades trigonométricas

de Gonzalo Tabare Hernandez Morales -
Número de respuestas: 2

Buenas, guiándome en la solución y luego de muchas cuentas llegué (creo que correctamente) a que 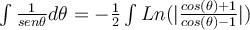\int \frac{1}{sen\theta}d\theta = -\frac{1}{2}\int Ln(\vert{\frac{cos(\theta)+1}{cos(\theta)-1}}\vert)
el tema es, ¿como hago para llegar a que 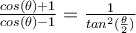\frac{cos(\theta)+1}{cos(\theta)-1}=\frac{1}{tan^2(\frac{\theta}{2})}?
probé con las identidades usuales pero no llegué a nada concluyente.
Gracias de antemano
En respuesta a Gonzalo Tabare Hernandez Morales

Re: Ejercicio 5, identidades trigonométricas

de Denis Gabriel Peña Presa -
En \vert{\frac{cos(\theta)+1}{cos(\theta)-1}}\vert el denominador es siempre menor a cero y el numerador mayor a 0 así que \vert{\frac{cos(\theta)+1}{cos(\theta)-1}}\vert = \frac{cos(\theta)+1}{1- cos(\theta)}

Ahora cos(\theta)=cos(\frac{\theta}{2} + \frac{\theta}{2})= cos^2(\frac{\theta}{2}) - sin^2(\frac{\theta}{2})
 
y 1= cos^2(\frac{\theta}{2}) + sin^2(\frac{\theta}{2}) así que sustituyendo queda


\frac{cos(\theta)+1}{1- cos(\theta)} = \frac{cos^2(\frac{\theta}{2}) - sin^2(\frac{\theta}{2}) + cos^2(\frac{\theta}{2}) + sin^2(\frac{\theta}{2})}{cos^2(\frac{\theta}{2}) + sin^2(\frac{\theta}{2}) - ( cos^2(\frac{\theta}{2}) - sin^2(\frac{\theta}{2}))} =\frac{cos^2(\frac{\theta}{2})}{sin^2(\frac{\theta}{2})} = \frac{1}{tan^2(\frac{\theta}{2})}

Espero haber ayudado, cualquier error avisenme