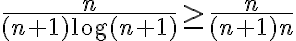Hola Ivan, creo que vas bien encaminado. Es cuestión de ordenar un poco las ideas nomás.
A la pregunta de si se puede comparar  con
con 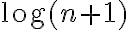 , te respondo que en principio podés comparar dos expresiones cualesquiera en tanto una acote (convenientemente, digamos) a la otra. Lo que necesitamos es que dicha acotación suceda, o bien para todo
, te respondo que en principio podés comparar dos expresiones cualesquiera en tanto una acote (convenientemente, digamos) a la otra. Lo que necesitamos es que dicha acotación suceda, o bien para todo  natural, o bien a partir de cierto
natural, o bien a partir de cierto  .
.
Dependiendo de si estamos probando que la sucesión es convergente o divergente el tipo de acotación necesaria. En este caso, como bien intuís, vas a poder probar que  acota superiormente a
acota superiormente a 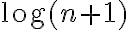 para
para  positivo. Esto te permite afirmar que
positivo. Esto te permite afirmar que
donde la desigualdad está en ese sentido porque la cota la tomamos en el denominador.
Tengamos en cuenta también que, al estar acotando nuestra serie por debajo y ser ésta de términos positivos, esto es útil sólo en caso de divergencia. Es decir, si la cota inferior que hallas diverge, también lo hará la serie original. Pero si converge, no te permite decir nada de la otra serie.
Al final dije más o menos lo mismo que vos, un poco más ordenado. Pero creo que con esto ya casi casi casi lo tenés resuelto.
Saludos.