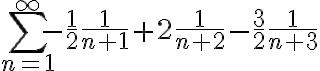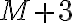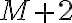Buenas! En este ejercicio plantee fracciones simples a ver si me facilitaba hallar la sucesión enésima para calcular el límite pero no me sirvió de mucho, logré verificar que es convergente pero me quedé trancada en la suma, alguna ayuda? gracias!
Hola Sol. Hoy en la consulta trabajamos con ese ejercicio y nos pasó algo similar. Probamos la convergencia y nos trancamos en hallar la suma. Resulta que aplicar fracciones simples sí sirve (pero hay que darse cuenta de cómo).
A través de la descomposición en fracciones simples podemos ver que la serie es telescópica, aunque la forma en que se cancelan los miembros no es evidente. Tomando como punto de partida la serie expresada de esta nueva forma, es decir
En la imagen que adjunto, se puede ver como quedan los términos a partir de un cierto 
arbitrario, y en particular, como se cancelan entre sí los que son del mismo color y están tachados. Se van cancelando en diagonal, con lo que quedan tres sumandos al principio, y otros dos al final (que tienden a cero).
Muchas gracias!!
Buenas noches! No me quedo claro la parte de n=M, a mi me estarían quedando solo lo que esta en verde y violeta. No entiendo como quedan los ultimos 2 terminos
Hola Yésica,
No se cancelan porque no hay otro término con denominador
y para el término con denominador 
sí existe otro sumando con ese denominador pero no es el opuesto. Tal vez te puede ayudar escribir 
como 
, y por lo tanto escribir la serie como suma de dos telescópicas.
Saludos,
Leandro
No se cancelan porque no hay otro término con denominador
y para el término con denominador sí existe otro sumando con ese denominador pero no es el opuesto. Tal vez te puede ayudar escribir como , y por lo tanto escribir la serie como suma de dos telescópicas.Saludos,
Leandro
Buenas;
No me queda claro como llegas al resultado, te comparto lo que yo hice y no me doy cuenta que termino cancela a cual. Podras ayudarme?
Graciass!
No me queda claro como llegas al resultado, te comparto lo que yo hice y no me doy cuenta que termino cancela a cual. Podras ayudarme?
Graciass!
Hola Nahuel,
Creo que te va a resultar más sencillo escribir solamente
, 
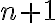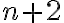y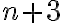 
en el denominador. Luego para cada caso te van a aparecer tres veces y se van a cancelar, salvo dos del principio y dos del final. En definitiva, te va a quedar lo que escribió Verónica.
De todas formas te recomiendo también escribir 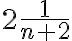como , y por lo tanto escribir la serie como suma de dos telescópicas, y ahí te va a salir directo.
Saludos,
Leandro
Creo que te va a resultar más sencillo escribir solamente
, y en el denominador. Luego para cada caso te van a aparecer tres veces y se van a cancelar, salvo dos del principio y dos del final. En definitiva, te va a quedar lo que escribió Verónica. De todas formas te recomiendo también escribir
como 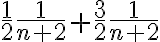, y por lo tanto escribir la serie como suma de dos telescópicas, y ahí te va a salir directo.Saludos,
Leandro