Foro Práctico 3

Hay algunos problemas en el planteo. Parecería que estás probando que toda sucesión contenida en $A$ tiene una subsucesión que tiende a $L$, lo cual no es cierto (y es bastante fácil construir contraejemplos. Por otro lado, no apunta exactamente a lo que queremos probar.

Lo que queremos probar, en palabras, es que $L$ es el supremo de $A$. Nuestras hipótesis nos dicen:

• $A$ está acotado superiormente y es no vacío: esto nos garantiza la existencia del supremo, que es la menor de todas las cotas superiores. Lo que aún no probamos es que el supremo es $L$
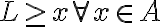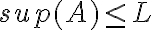• $L \geq x \forall x \in A$: Esto quiere decir que $L$ es una cota superior de $A$. O sea que $sup(A) \leq L$. Nos estaría faltando ver que además $L$ es la menor de dichas cotas.
• Existe una sucesión cuyos términos están incluidos en $A$ que converge a $L$. Este es quizás el paso más sensible y con el que hay que jugar un poco con la definición de supremo. Pero a grandes rasgos la idea es que el hecho de poder acercarnos tanto como querramos a $L$ a través de puntos de $A$ significa que $L$ no puede estar "lejos" del conjunto. 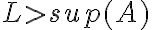Una estrategia posible sería asumir por absurdo que $L> sup(A)$ y llegarías a que necesariamente hay puntos de la sucesión dada que se "escapan" de $A$.